The Mathematics of the Genetic Code

As a student of both biology and computer/information science (CIS), I sometimes see similarities between living and man-made systems. I recently cracked open a microbiology textbook and began reading about DNA and RNA replication and protein synthesis in a cell. To put it simply, DNA contains the genetic code, RNA carries a copy of that code and acts as a "messenger", and ribosomes within the cell read the RNA and help create the proteins. The RNA genetic code is made up of four nucleotides: A (adenine), C (cytosine), G (guanine), and U (uracil). These nucleotides are read in groups of three (a codon) and the codon instructs the cell to add a particular amino acid to the chain in the process of creating a polypeptide protein. For example, reading a GCA codon will cause Alanine to be added to the chain. Combine lots of amino acids and you eventually get proteins which can make muscles and and other structures in the body.

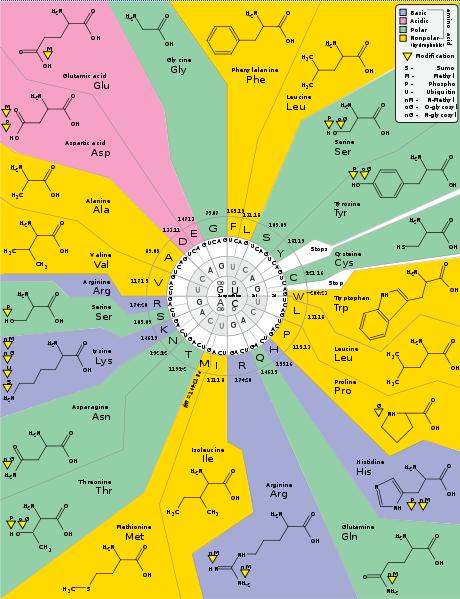
The key fact here is that there is a particular code for each amino acid. The G, C, and A nucleotides have no particular meaning by themselves, but when they are read in sequence at the right time Alanine is assembled onto the polypeptide. As a student of CIS, it occurred to me that this code could be described with mathematics. In a computer system, everything at the lowest level is binary, which is a base-2 numbering system using the symbols "1" and "0". So what was the base numbering of the genetic code? If you think of the four different nucleotides as just symbols (AUGC) then you could describe it as a base-4 numbering system. Since each codon has only 3 letters, then there are 4^3 different codon combinations. Think of this as 4*4*4 which is equal to 64. So does this mean RNA can specify up to 64 different amino acids? No, there are only 22 different amino acids which can be assembled within cells. Why is that? Because 1, 2, 3, 4, or even 6 different codons can translate to the same amino acid. The chart above was found on Wikipedia. It will give you a good sense of what I have just described.

What is fascinating about this code is that there is a START codon (AUG) and three STOP codons (UGA, UAA, and UAG) which tell the ribosome where the beginning and end of the code are on a gene. This is much like the BOF (beginning of file) and EOF (end of file) markers on a computer data tape! In a computer, errors in data transmission can be corrected using several methods. One method is CRC (Cyclical Redundancy Check). Within a cell there are also mechanisms by which an error in genetic code transcription is corrected - but the method is quite different. But not all genetic errors (sometimes called mutations) are corrected. This fact is the very reason why organisms evolve and change over time. Some mutations can be fatal, but others can give an organism an advantage and help it survive.

As scientists continue to study genetic sequences I imagine that more similarities between genetic codes and computer codes will be found. The human genome, for example, probably contains useful code, garbage code (which has no particular function), obsolete code (genes for characteristics we have lost through evolution, such as a primate tail), and maybe even code which can clearly be classified as data or instructions.

In his book A New Kind of Science, Stephen Wolfram described the concept of "the simplest universal Turing machine". A universal Turing machine is a computational model which can do "any computation which can be done". Such a machine was discovered by a 20-year-old undergraduate student (Alex Smith) from Birmingham, UK. Smith described a 2,3 machine which has 2 states and 3 colors. Without going into detail about what that means, it is adequate to say that it is simple - but deceptively simple! When the machine springs into action it can create mind-bending complexity. It is not inconceivable that such a machine could be implemented using the genetic mechanisms of a cell. It would be even more amazing if we found a "natural" version of this Turing machine already coded into the genes of a living organism. Wolfram suggests this possibility in his book.