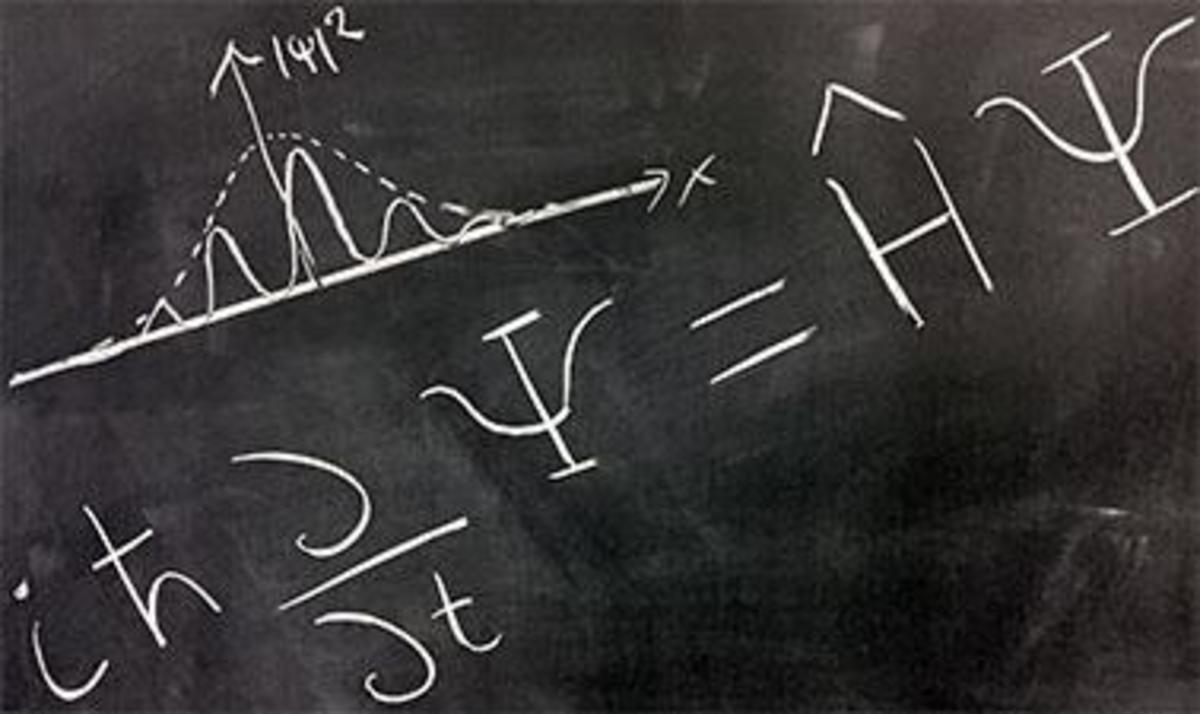The Schrodinger's Wave Equation


Born in Vienna, Austria on 12th August 1887, Erwin Schrodinger came from a very erudite background where his father was well versed in in both Italian painting and chemistry. Erwin himself not only appreciated science but also admired ancient German poetry. He received his education in the University of Vienna where he met his mentor Fritz Hasenöhr. Later, Schrodinger found himself a position in the University of Zurich where he worked on several projects for 6 years. It was in the University of Zurich that Schrodinger unfolded his famous, Schrödinger's wave equation to the scientific community in 1926.
Although scientists like de Broglie, Heisenberg and Max Planck had proposed that submicroscopic particles like an electrons had dual nature -particle like and wave like, yet they had no mathematical equations to further substantiate their claims. A need for mathematical equations was felt to explain new information about atoms. Schrodinger was the first man to take advantage of this opportunity and formulated the famous Schrödinger's wave equation. The Schrodinger equation is simply an equation that demonstrates wave properties of matter.
Erwin Schrödinger, explored the consequences of these matter waves and proposed a wave equation analogous to the known equations for other wave motions in nature from classical physics. This wave equation describes how a wave associated with an electron or other subatomic particle varies in space and time as the particle moves under various forces. Schrödinger's equations worked out the exact solutions of the wave equation for the hydrogen atom, and the results perfectly agreed with the known energy levels of these atoms, seemingly without any of the complications and metaphysical speculations associated with Heisenberg's uncertainty principle. Moreover, the equation could also be applied to more complicated atoms, and even to particles not bound in atoms at all. It was soon found that in every case, Schrödinger's equation gave a correct description of a particle's behaviour, provided it was not moving at a speed near that of light. Despite his success, the very meaning of the waves remained unclear. Schrödinger believed that the intensity of the wave at a point in space represented the 'amount' of the electron that was present at that point. In other words, the electron density was spread out, rather than being concentrated at one single point. However, this contradicted the basis of matter waves where particles were defined to be localized. A wave on the otherhand is delocalized and when a wave, representing an electron, strikes a target, it spreads out in all directions. Experiments indicated that an electron scatters in some specific direction but never breaks up. Max Born, another German physicist as also a good friend of Einstein, interpreted this result as follows with the concept of probability density. He considered that the wave associated with the electron is not entirely a tangible 'matter wave', but a wave that determines the probability of scattering of the electron in different directions. The region in which this associated matter wave has a large amplitude, the probability of finding an electron there is high. However under any circumstances one could find the whole particle, and not parts of it. This indicated that the simple interpretation of the wave equation as a physical matter waves in ordinary space, as was originally assumed by Schrödinger, is incorrect. Born concluded that matter waves represent probability amplitudes associated with the occurrence of an event. If there are multiple alternatives for the event to happen, the total amplitude is the sum of the alternative amplitudes. The absolute square of the overall amplitude, the intensity of the wave, must be interpreted as the probability that the event will happen. This was the function Ψ2 the probability density.Thus Max Born reduced Schrödinger's equation completely into probabilistic terms. Schrödinger was reluctant to accept this interpretation. This difference between the world of the very small and the everyday world we experience cannot be understated.When you are walking across a street and an automobile is approaching you, it is at a definite place at any given time, and it is possible to describe with a great deal of precision where exactly the automobile is, and where it will be at another moment in time if it continues on the same path. For objects in the submicroscopic realm, this is not true. The importance of the introduction of statistical probabilities into physical law cannot be understated as earlier Newtonian physics, had no place for probabilities. In the Newtonian world-view, an object of any kind could at least in theory be described as having a definite position at any given time. In Quantum theory, when dealing with particles such as electrons, protons and neutron, the probabilities describing material particles can never be replaced by classical newtonian definitions of position. Applying these points to an electron in an atom, nevertheless, we see that the electron is no longer a point in space moving along a definite path, but a cloud of probabilities . To every point in a light wave we can attach a numerical probability (per unit time interval) that a photon can be detected in any small volume centred on that point, and light is viewed as a probability wave. The Schrodinger equation is a solution to this equation which describes the quantum aspects of a system. However, physically interpreting the wave is one of the main philosophical problems of quantum mechanics.
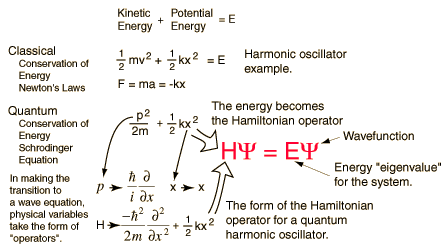
The solution to the Schrodinger equation is based on the method of Eigen Values devised by Fourier. This is where any mathematical function is expressed as the sum of an infinite series of other periodic functions. The trick is to find the correct functions that have the right amplitudes so that when added together by superposition they give the desired solution. So, the solution to Schrondinger's equation, the wave function for the system, was replaced by the wave functions of the individual series, natural harmonics of each other, an infinite series. Shrodinger has discovered that the replacement waves described the individual states of the quantum system and their amplitudes gave the relative importance of that state to the whole system.
Schrodinger's equation demonstrates all of the wave like properties of matter and was one of greatest achievements of 20th century science. It is used in physics and most of chemistry to deal with problems about the atomic structure of matter. It is an extremely powerful mathematical tool that rebuilds the basis of wave mechanics.
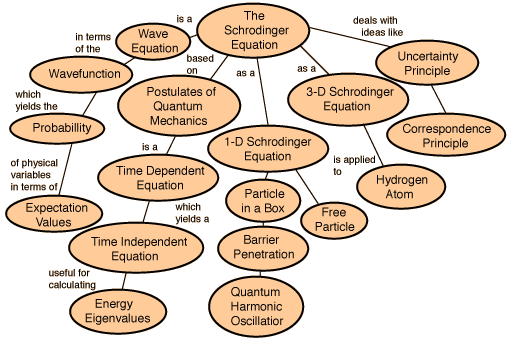
The Schrodinger equation has a time dependent equation used for describing progressive waves, applicable to the motion of free particles. And the time independent form of this equation used for describing standing waves.
Schrodinger’s time-independent equation can be solved analytically for a number of simple systems. The time-dependant equation is of the first order in time but of the second order with respect to the co-ordinates, hence it is not consistent with relativity. The solutions for bound systems give three quantum numbers, corresponding to three co-ordinates, and an approximate relativistic correction is possible by including fourth spin quantum number.
Schrodinger was the first person to write down such a wave equation. Much discussion then centred on what the equation meant. The eigenvalues of the wave equation were shown to be equal to the energy levels of the quantum mechanical system, and the best test of the equation was when it was used to solve for the energy levels of the Hydrogen atom, and the energy levels were found to be in agreement with Rydberg's Law.
The Schrodinger equation is used to find the allowed energy levels of quantum mechanical systems such as atoms. The associated wave function gives the probability of finding the particle at a certain position.