The Walsh Hadamard Transform
The Walsh Hadamard Transform
The Walsh Hadamard Transform (WHT) has the effect of spreading out a point in the input space into a sequency pattern in the output space. The sequency patterns of 2 or more points in the input space add together in the output. Likewise if a sequency pattern is present in the input space a point will be present in the output space.
Figure 1

Figure 2

The term sequency indicates the number of sign transitions in the output when a particular point is transformed. As you can see the sequencies occur in an irregular pattern.
Applying the WHT twice gives you back your original data multiplied by a constant c. In practice each WHT is usually multiplied by a scaling factor (1 over the square root of c) during calculation to avoid the need for repeated scale adjustments.
Calculation
The WHT is nearly always done on input data that is positive integer power of 2 long. For example a 2-point transform, a 4-point transform, an 8-point transform etc. A 12-point WHT is possible along with some other rare possibilities but usually you are confined to powers of 2.
The 2-point WHT is rather simple. It is the sum and difference of the 2 input numbers. To do the 4 point transform pair up the input data and form the sum and difference of each pair. Then form the sum and difference of the 2 sum terms and form the sum and difference of the 2 difference terms.
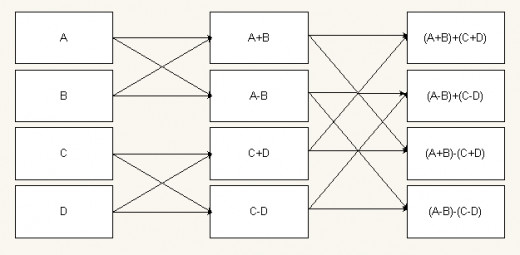
There are two principle algorithms for computing the WHT. The Butterfly algorithm and the Split-Array algorithm (see figure 3 and figure 4).
Figure 3
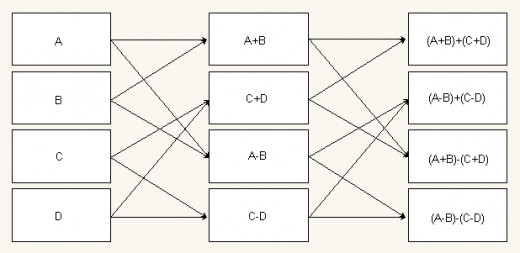
Figure 4
Sequency
The sequency a particular point corresponds to is the Gray Code of it's bit reversed index value. The code fragments in figure 5 show how to calculate both the Gray code and it’s inverse. The sequency basis of the WHT can also be generated using logic operations, see figure 6. This provides an alternative way of calculating the WHT.
Figure 5

Figure 6

Mathematical Properties
For the properly scaled WHT the following mathematical properties apply:
- The vector length of the output is the same as the input.
- The central limit theorem applies to each of the outputs of the WHT since they are merely sums and differences of the inputs.
- The WHT will transform random data from almost any probability distribution into data with a Gaussian/Normal distribution.
- If x=s+WHT(s) and y=s-WHT(s) then 2s=x+y, 2WHT(s)=x-y
- A series of random permutations and WHT’s will map a point on the surface of a hyper-sphere to another random point (uniformly) on the surface of the hyper-sphere. A WHT transforms a point to a sequency pattern. A random permutation will break up that sequency pattern (except sequency 0) into a list of randomly chosen numbers. The central limit theorem will apply when you do another WHT.
- While the WHT is not very useful for data compression in itself, selecting out high magnitude values in the intermediate steps of calculating the WHT can provide a reasonable data compression algorithm.
- The composition of a WHT and a permutation with the output feed back into the input provides a complicated resonance chamber that can be used for pattern detection.



