The measurements of a circle(Circumferance, Area of a circle and a sector, Perimeter of a sector
Circles
In this hub we are going to be
looking at the different parts of a
circle and how to calculate each
of them.
The Circumference of a Circle,
this is the perimeter of a circle.
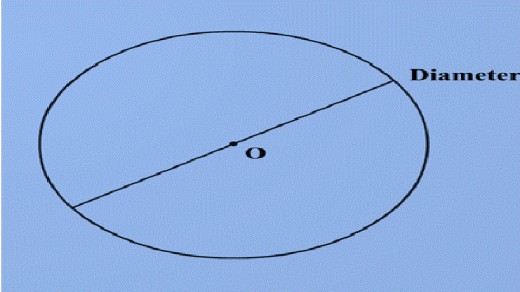
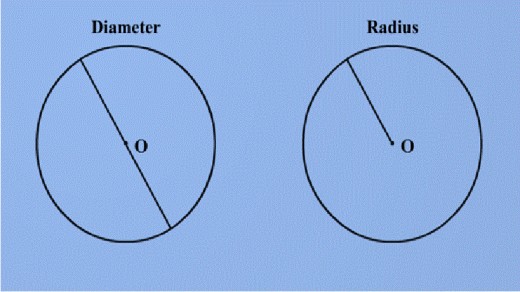
The Diameter = 2 radii
(twice the radius)
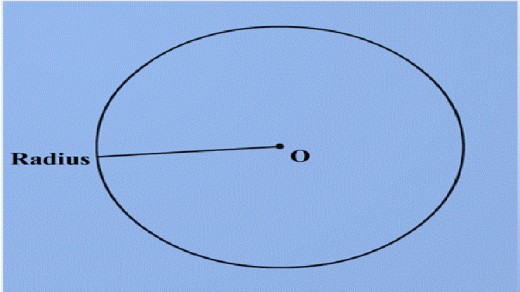
The Radius is half
the Diameter
PERIMETER of a Circle
The formula for the circumference
of a Circle is;
C = TT D C = 2 TT r
(C = TT x D ) ( C = 2 x TT x r)
- The Pi (TT) = 3.141592654
(check this on a calculator)
- (Pi is a special number used to
calculate distance and area
when dealing with a circle)
- Your told that the Diameter is 12cm in the above diagram,
and you have to find the Circumference to 1 decimal
place.
C = TT D
C = TT x 12 = 37.699... (use your calculator)
C = 37.7 (1 decimal place) ANSWER
2. If the diameter was 12cm that makes the Radius 6cm
So now we'll calculate the circumference of the same circle
using the Radius and you have to find the Circumference to
1 decimal place.
C = 2 TT r
C = 2 x TT x 6 = 37.699....(use your calculator)
C = 37.7 (1 decimal place) ANSWER
AREA of a Circle
The Area of a Circle is represented by the formula;
A = TT r2
So using the Circle above as an example;
We know that the Radius is 6cm (½ the Diameter which is 12cm)
A = TT r2
A = TT x 62
A = 113.0973355
A = 113.1cm2 ( 1 d. p.) ANSWER
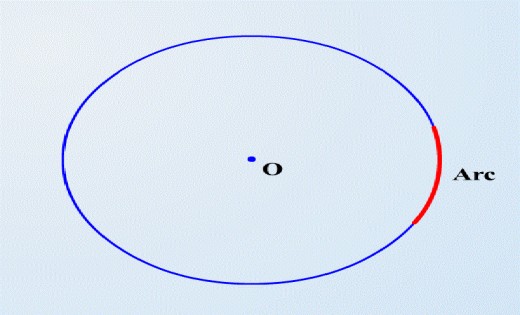
The red marked part of the circle
is known as an Arc
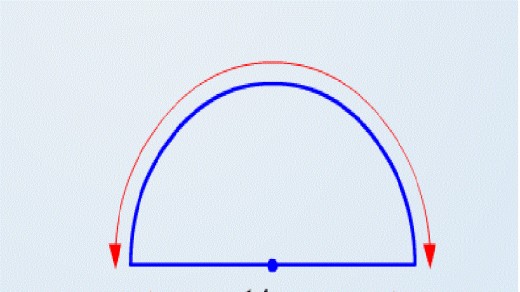
PERIMETER of a Semi-Circle
If the arc is a semi-circle our
formula will be C = ½ TT D
- We are asked to find the Perimeter of this Semi-Circle correct to 1 decimal place, and we are told the Diameter is 6cm.
Now the Perimeter is made up of the Arc(marked with red arrow)
plus the Diameter. So it's two parts to find the Perimeter of this
Semi-Circle.
(i) C = ½ TT D (½ because it's a Semi-Circle)
C = ½ x TT x 6 (do this on your calculator)
C = 9.42477
(ii) Perimeter = 9.42477 + 6 = 15.42477
= 15.4 ( 1 d. p.) ANSWER
AREA of a Semi-Circle
Here we are finding the Area of a Semi-Circle.
Using the example above we know our Diameter is 6cm
So the Radius will be 3cm (½ the Diameter)
To find the Area of a Semi-Circle we use the following formula;
A = ½ TT r2
A = ½ x TT x 32
A = 14.137166...
A = 14.1cm2 ( 1 d.p.) ANSWER

PERIMETER of a Quadrant
A Quadrant is a ¼ of a Circle.
If the arc is a Quadrant our
formula will be C = ¼ TT D
We are asked to find the Perimeter of this Quadrant correct to 1 decimal place, and we are told the Radius is 8cm.
The Diameter is twice the Radius;
Therefore the Diameter is 16cm
Now the Perimeter is made up of the Arc
plus the two Radii ( These need to be
added on at the end to the perimeter of
the Quadrant's arc to find the total Perimeter of the Quadrant.
So it's two parts to find the Perimeter of
this Quadrant.
(i) C = ¼ TT D ( ¼ because its a Quadrant)
C = ¼ x TT x 16
C = 12.56637061 (Perimeter of the arc)
(ii) Perimeter of Arc + Radii + Radii
Perimeter = 12.56637061 + 8 + 8 = 28.566.......
= 28.6 ( 1 d. p.) ANSWER
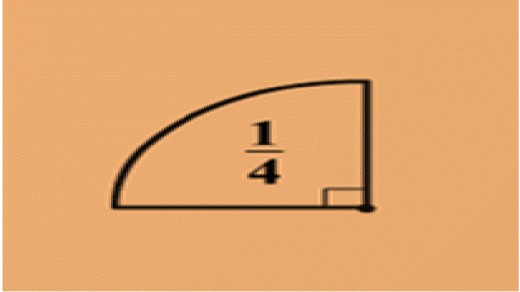
AREA of a Quadrant
Here we are finding the Area of a Quadrant.
Using the example above we know our Diameter is 16cm
So the Radius will be 8cm (½ the Diameter)
To find the Area of a Quadrant we use the following formula;
A = ¼ TT r2 (¼ as its a Quadrant)
A = ¼ x TT x 82 (use your calculator)
A = 50.2654......
A = 50.3 cm2 ( 1 d.p.) ANSWER
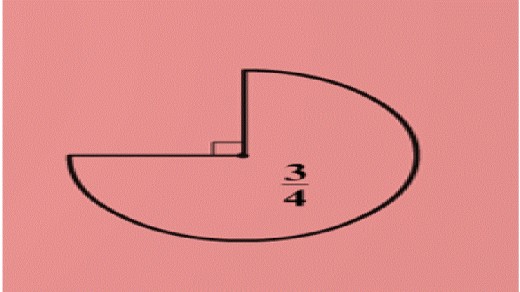
PERIMETER of Three Quadrants
This Quadrant is a ¾ of a Circle.
Our formula will be C = ¾ TT D
- We are asked to find the Perimeter of this Quadrant correct to 1 decimal place, and we are told the Radius is 10m.
- The Diameter is twice the Radius;
Therefore the Diameter is 20m
Now the Perimeter is made up of the Arc
plus the two Radii ( These need to be
added on at the end to the perimeter of
the Quadrant's arc to find the total Perimeter of this Quadrant.
So it's two parts to find the Perimeter of
this Quadrant.
(i) C = ¾ TT D ( ¾ because its three Quadrants)
C = ¾ x TT x 20
C = 47.1238898 (Perimeter of the arc)
(ii) Perimeter of Arc + Radii + Radii
Perimeter = 47.1238898 + 10 + 10 = 67.123...
= 67.1m (1 d.p.)
AREA of Three Quadrants
Here we are finding the Area
of this Quadrant. It has a value
of three Quadrants = ¾
Using the example above we know our Diameter is 20m
So the Radius will be 10m (½ the Diameter)
To find the Area of this Quadrant we use the following formula;
A = ¾ TT r2 (¾ as its three Quadrants)
A = ¾ x TT x 102 (use your calculator)
A = 235.619....
A = 235.6m2 ( 1 d.p.)
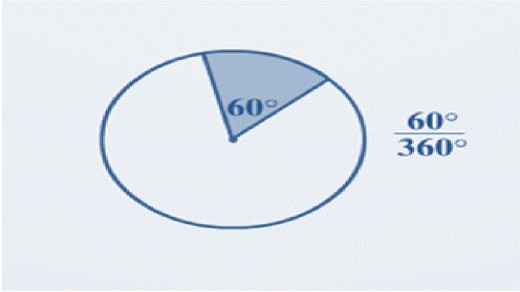
PERIMETER of a Sector
Here we are finding the Perimeter
of a Sector, it has a value of
60 degrees.
- We are asked to find the Perimeter of this Sector correct
to 2 decimal places, and we are told the Radius is 15m.
- The Diameter is twice the Radius;
Therefore the Diameter is 30m
Now the Perimeter is made up of the Arc
plus the two Radii ( These need to be
added on at the end, to the perimeter of
the Sector's arc to find the total Perimeter of this Sector.
- So it's two parts to find the Perimeter of
this Sector.
This time we need to look at the fact we're not dealing with a whole Circle.
- In fact we're dealing with a Fraction,
60 / 360 (60 degrees over the whole Circle)
This is the Fraction part, so let's put this into our formula for Perimeter.
(i) C = 60 / 360 TT D
C = 60 / 360 x TT x 30 (use your calculator)
C = 15.70796... (Perimeter of the arc)
(ii) Perimeter of Arc + Radii + Radii
Perimeter = 15.70796... + 15 + 15 = 45.707.....
= 45.71m ( 2 d.p's) ANSWER
AREA of a Sector
Here we are finding the Area
of this Sector, it has a Fractional
value of 60 / 360 , to two decimal
places.
Using the example above we know our Diameter is 30m
So the Radius will be 15m (½ the Diameter)
To find the Area of this Sector we'll use the following formula;
A = 60 / 360 TT r2
A = 60 / 360 TT 152 (use your calculator)
A = 117.809......
A = 117.81 m2 ( 2 d.p's.)