Symmetry in Physics for Dummies Like Me

What, exactly, is symmetry? Paraphrasing Richard Feynman (one of the absolute best popularizers of science of all time), who puts it pretty simply: you can do something to a thing, and it looks the same. Wikipedia puts it a bit more formally:

"A physical or mathematical feature of the system (observed or intrinsic) that is preserved or remains unchanged under some transformation."

Symmetry across the ages has always fascinated mankind, and it has fascinated me ever since I was old enough to put coherent thoughts together. On the surface, symmetry seems pretty simple. A human face has left-right symmetry, and a circle has radial symmetry. But there are more ways for things to be symmetric than the merely visual aspect, and that's where things get more interesting for me. Let's take a look.

As alluded above, there are several types of symmetry we're already intimately familiar with, or "wired" to experience. The most common form is left-right symmetry, as is evident in the human body (although it's not 100% perfect; your heart is on the left side of your chest, your left arm is slightly different from your right arm, and so on; but it's certainly very, very similar).

Another very intuitive concept is top-bottom, or up-down symmetry. A flying saucer has up-down symmetry, or a figure 8. You can think of top-bottom symmetry as left-right symmetry turned sideways.

Mirror symmetry can encompass both top-bottom and left-right symmetry. The human face is mirror-symmetric along the y axis (just another way of saying it's left-right symmetrical), and there's another form of left-right and top-bottom symmetry that doesn't involve mirror symmetry- think of it as "rubber stamp" symmetry if you'd like, and just imagine an exact duplicate on the left side and the right side.

Radial symmetry is intimately familiar to us. You can imagine a circle in two dimensions, or a sphere in three dimensions, for the perfect radially symmetric visual device. Some shapes have discrete symmetry, like a square, where it depends on how you look at it from the center. A circle is symmetric no matter how many degrees you go out from the center; a square is not.

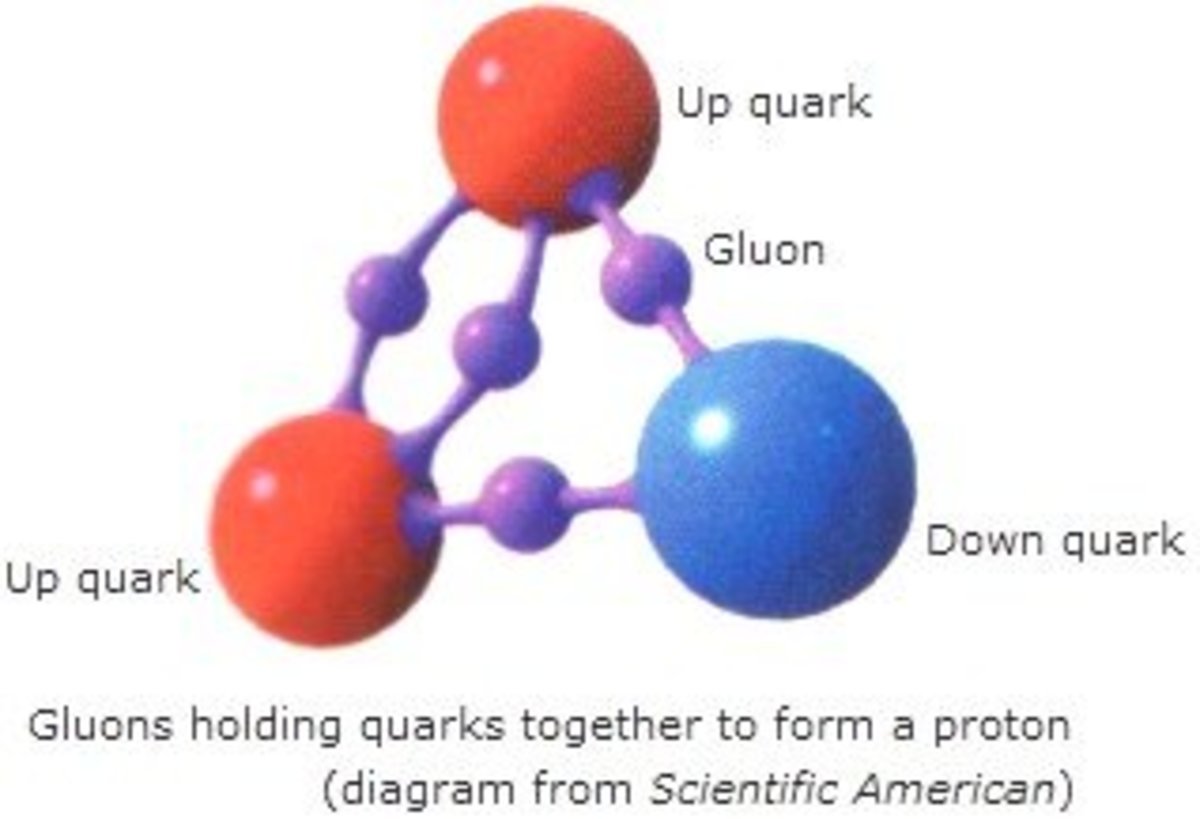
The above forms of symmetry are spot on, just perfect. But there's an "almost symmetry" that's often found in nature. One such example of this "almost symmetry" is the mass of the neutron and the proton, which is now far better understood than it was, say, in the 1950s (before the quark model). Why were the neutron and proton so very close in mass, when the electron was 1836 times smaller than the proton, but the neutron is only 1.001 times bigger than the proton.

While we're talking about protons and neutrons, there's another type of symmetry we can pretty easily understand. Protons are attracted to other protons via the strong nuclear force in exactly the same way that protons are attracted to neutrons. This observation was certainly significant in understanding what was going on within the nucleus of the atom, but what we need to understand is this kind of "force symmetry" the two different interactions have (proton-proton and proton-neutron). Although the proton is positively charged and the neutron is, of course, neutral, the two particles share the same strong force of attraction.

During the discoveries in the late 1950s and early 1960s at various particle accelerators (especially Brookhaven), physicists noticed that there were other similar "families" of particles, where it didn't matter if you switched out one for the other in terms of the attractive nuclear forces felt by these particles. These families can be visualized as rows in a grid, with the proton and neutron being at the top of the grid. A particle called the "cascade" particle (as described by Richard Feynman in the associated video) fits two rows beneath the proton and neutron, because it goes through two steps to decay into a proton or neutron (the step in between is the sigma). Given that these particular particles decayed in the steps as they did, could this particular method of decay be used to predict other particles in other grids? It could, and that is what the "omega minus" particle discovery was all about, as Feynman so eloquently explains at the beginning of the BBC special.

Sure, symmetry is aesthetically beautiful. The human eye is naturally attracted to the symmetry of a face, as is evidenced in art throughout the ages. We're attracted to symmetry for genetic reasons, too. However, as is evidenced by the discovery of the "omega minus" particle, there's a great deal more scientific use from the study of symmetry as well, particularly abstract symmetries. One such extrapolation lies in a symmetry between the forces of nature. Photons are the quanta, or individual force-carrying particles, of the electromagnetic force. In other words, magnetism and electricity work because of a photon flying back and forth between two objects that are attracted or repelled. With the weak force, it was discovered that W and Z bosons cause the force to work, or mediate it. The strong force, likewise, has gluons (physicists are such nerds!). It is hypothesized that gravity works via gravitons, although there is no evidence yet to support this concept.

It's impossible to say what our next big discovery based on symmetry will be, but it's a safe bet that we will, indeed, make discoveries based on the principles of symmetry. Me, I'd just like to continue to think about this stuff as I drift off to sleep!