Triangle Geometry Review, Practice Problems with Solutions for GMAT
Our topic in this hub is to review triangle geometry concepts, rules and formulas and then cover 6 practice questions to excel on the subject to get ready any question comes in this area in GMAT exam.
NOTE: Due to limitation to display line segment symbol over line in html, line segment will be only named as their start and end point letter.
Triangle
TRIANGLE REVIEW
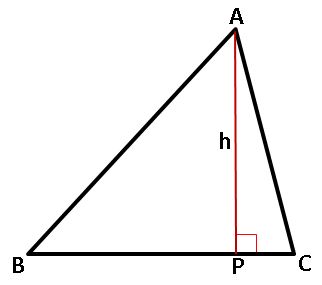
A triangle is a polygon with 3 vertices and 3 sides. Triangle on the right is denoted as ΔABC. A, B and C are vertices. AB, AC and BC are sides of the triangle.
Area (1/2) * BC * h
Perimeter AB + BC + AC
Triangle
Rule 1
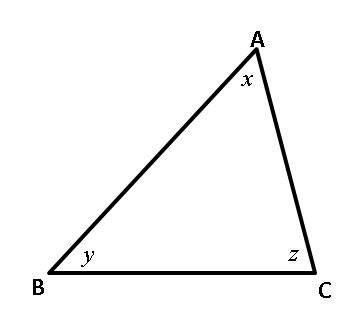
The sum of interior angle of a triangle is 180ο
x + y + z = 180ο
Rule 2
Any side of the triangle length is always less than sum of the length of other sides.
AC < AB + BC
AB < AC+ BC
BC < AB + AC
Equilateral Triangle
Rule 3
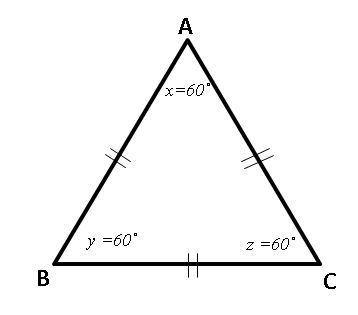
All sides and angles of an Equilateral Triangle are equal. All angles are 60ο
<A = <B = <C = 60ο
AB = BC = AC
Isosceles Triangle
Rule 4
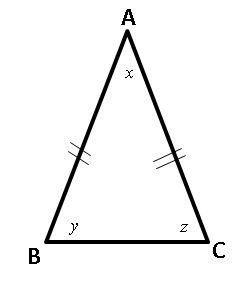
An isosceles triangle has 2 interior angles equal measure and opposite side of those angles are same length.
<y = <z
AB = AC
Right Triangle
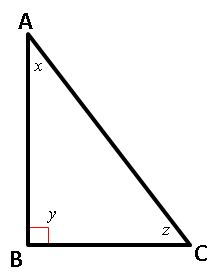
Rule 5
If a triangle has a right angle, it is called right triangle.
y = 90ο
Hypotenuse Rule AB2 + BC2 = AC2
Known whole number length for right triangle are
32 + 42 = 52 (3:4:5 ratio)
52+ 122 = 132 (5:12:13 ratio)
Area ABC = (1/2) * AB * BC
When angles of a right triangles are 45ο : 45ο : 90ο sides ratio will be 1:1:√2
When angles of a right triangles are 30ο : 60ο : 90ο sides ratio will be 1:√3:2
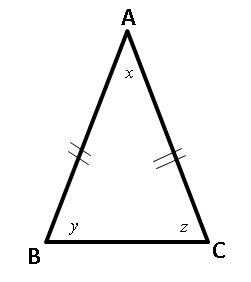
Figure for Practice Question 1
PROBLEM SOLVING PRACTICE QUESTIONS
1) ΔABC is an isosceles triangle AB=AC. What is x terms of y ?
a) 180 - y
b) 90 + y
c) 90 - y
d) 180 - 2y
e) 60 + y
Solution 1: The sum of inner angles of an triangle is 180ο.
x+y+z = 180
since y=z in isosceles triangle we can replace z with y from above equation
x + y + y = 180
x + 2y = 180
x = 180 -2y
The correct answer is D.
Figure for Practice Question 2
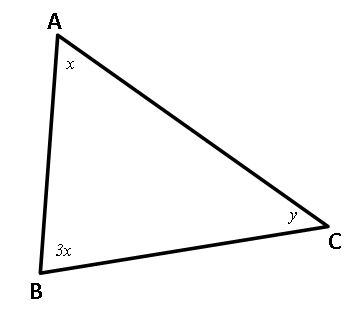
2) In ΔABC triangle on the right, if x : y ratio is 1 : 4 then x = ?
a) 15
b) 20
c) 22.5
d) 32.5
e) 35
Solution 2: From the ratio 4x = y.
The sum of inner angles of an triangle is 180ο.
x + 3x + 4x = 180
8x = 180
x = 180/8
x = 22.5
The correct answer is C.
Figure for Practice Question 3
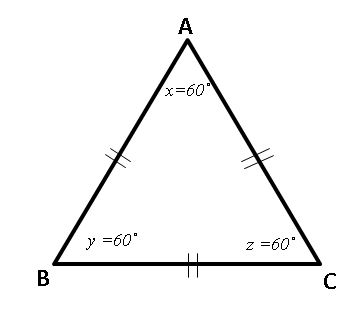
Figure for Practice Solution 3
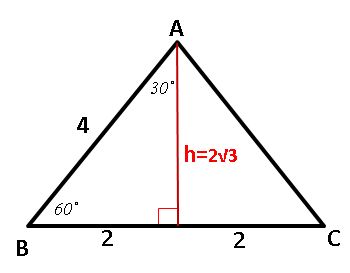
3) ΔABC is an equilateral triangle and the length of the side is 4. What is the area of the triangle?
a) 8
b) 12
c) 6√3
d) 4√3
e) 8√2
Solution 3: If we draw the height line, we end up special 2 right triangle. Each right triangle has special 1:√3:2 ratio.
See the figure right side.
Area = (1/2) * BC * h = (1/2) * 4 * 2√3 =4√3
The correct answer is D.
Data Sufficiency Practice Questions
1) What is the area of a triangle?
(1) The sides are 3, 4 and 5
(2) One of the vertices is 90ο
Solution 1:
Statement (1) requires such triangle to be an right triangle. 3 and 4 must be the length and 5 is the hypotenuse. Multiplication of legs and divide by 2 will give the area of the triangle.
Statement (2) without knowing Statement (1) is not sufficient to know the area of the triangle.
The correct answer is A.
Figure for Data Sufficiency Question 2
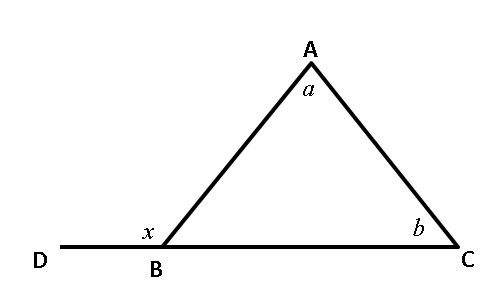
2) BCD is straight line. What is X=?
(1) a = 50ο
(2) AB = AC
Solution 2: Statement (1) alone is not sufficient to find out X.
Statement (2) alone is not sufficient to find out X.
Let us try to use both information together. If we know a=50ο and triangle is isosceles then Angle B and C is equal and (180 - 50)/2=65 since 65+x = 180. We can find X as 115ο
The correct answer is C.
Figure for Data Sufficiency Question 3
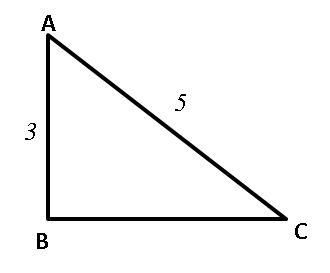
3) ΔABC is a triangle and the length of side BC is whole number.
What is the length of BC ?
(1) Angle B= 90ο
(2) Angle A is smaller than angle B and bigger than angle C
Solution 3:
Statement 1 requires the triangle to be an right triangle. by using formula we can find BC= 4
Based on Statement (2) 3 < BC < 5
BC is equal to 4.
Both Statements are alone is sufficient to solve the problem.
The correct answer is D.



