How to Solve for Properties and Proofs of the Triple Scalar Product of Vectors for Calculus

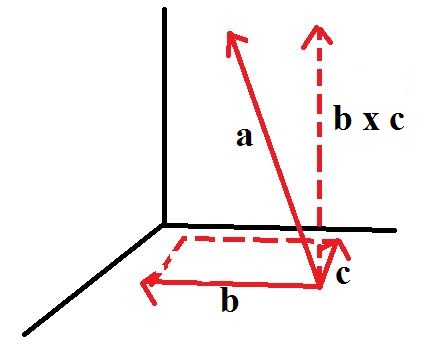
The triple scalar product (TSP) is a unique blend of the dot product and the cross product, two very important operators in mathematics. It has a similar origin as the cross product, which was found when looking at the area of a parallelogram contained within two vectors. The TSP differs however, for its derivation is found by taking the volume of a parallelepiped (a 3-D object whose faces are made up of parallelograms) set by three vectors that are not in the same plane.

If vectors b and c make up the base of the parallelepiped, then we would have a parallelogram and we know from an earlier article that the area of a parallelogram is the magnitude of the cross product between the vectors, or that

Area of the base = || b x c ||

Now, what is the height of the parallelepiped? Well, it will be however much of the a vector is vertical to the base vectors. But how can I know how much of the vector that will be? When I take the cross product, I get a vector that is orthogonal to both b anc c. This vector will be in the direction of a. If I know how much a projects onto b x c then I will know its component in the vertical direction and hence the height. Therefore,

Height = || proj_{b x c}a ||

Or that the height of the parallelepiped is the magnitutde of the projection of a onto b x c.

Now I can find the volume.

Volume = Area of base times the height

= || b x c || || proj_{b x c}a ||

But we know from an earlier article that proj_{b x c}a = (b x c) [a ∙ (b x c)] / (||b x c||²) so

|| b x c || || proj_{b x c}a || = || b x c || ||(b x c) [a ∙ (b x c)] / (||b x c||²) ||

But note that

||(b x c) [a ∙ (b x c)] / (||b x c||²) || = ||[(b x c)/||b x c||] [a ∙ (b x c)] / ||b x c|| ||

And (b x c)/||b x c|| is just a unit vector in the direction of b x c. Again, from an earlier article we know that the magnitude of a unit vector is 1 so we can simplify the volume equation to

|| b x c || ||[a ∙ (b x c)] / ||b x c|| || = ||b x c|| | [a ∙ (b x c)] / ||b x c|| |

We now write the second term with absolute value bars because in removing the unit vector all we have left is a scalar, and the magnitude of a scalar is just a scalar (just as [5²]^0.5 is simply 5) but all we want is the positive value since we are dealing with a volume. Hence the bars. Now notice that we have a ||b x c|| in the numerator and the denominator, so they cancel and all we are left with is

|a ∙ (b x c)|

We call this term inside the absolute value bars the triple scalar product and the volume is just the absolute value of this. Note that the TSP is not a vector but a scalar, like the dot product and unlike the cross product (Larson 795).

So what does the TSP look like when I try to get a value for it? If we expand it, we shall find out.

a ∙ (b x c) = a ∙ [i(b₂c₃ – b­₃c₂) - j(b₁c₃ – b­₃c₁) + k(b₁c₂ – b­₂c₁)]

=(a₁i + a₂j + a₃k) ∙ [i(b₂c₃ – b­₃c₂) - j(b₁c₃ – b­₃c₁) + k(b₁c₂ – b­₂c₁)]

=a₁(b₂c₃ – b­₃c₂) - a₂(b₁c₃ – b­₃c₁) + a₃(b₁c₂ – b­₂c₁)

Which we will notice is the same thing as

| a₁ a₂ a₃ |

| b₁ b₂ b₃ |

| c₁ c₂ c₃ |

Therefore, the TSP is simply the determinant of a matrix with components of a, b, and c (794).

Note that order is important. Simply switching two rows in the matrix will completely change the answer. In fact, by doing so you change the signs to the opposite operation. To see this, look at the TSP of b ∙ (a x c). This would have the following matrix that has two rows switched from before:

| b₁ b₂ b₃ |

| a₁ a₂ a₃ |

| c₁ c₂ c₃ |

Then that determinant would be

b₁(a₂c₃ - a­₃c₂) - b₂(a₁c₃ - a­₃c₁) + b₃(a₁c₂ - a­₂c₁) = b₁a₂c₃ - b₁a­₃c₂ - b₂a₁c₃ + b₂a­₃c₁ + b₃a₁c₂ - b₃a₂c₁

= b₃a₁c₂ - b₂a₁c₃ - b₃a₂c₁ + b₁a₂c₃ - b₁a­₃c₂ + b₂a­₃c₁

By the commutative property. Now If I pull out the common a terms then

b₃a₁c₂ - b₂a₁c₃ - b₃a₂c₁ + b₁a₂c₃ - b₁a­₃c₂ + b₂a­₃c₁ = a₁(b₃c₂ - b₂c₃) - a₂(b₃c₁ + b₁c₃) + a­₃(b₁c₂ + b₂c₁)

= -a₁(b₂c₃ - b₃c₂) + a₂(b₁c₃ - b₃c₁) - a­₃(b₂c₁ - b₁c₂)

= (-1) [a₁(b₂c₃ – b­₃c₂) - a₂(b₁c₃ – b­₃c₁) + a₃(b₁c₂ – b­₂c₁)]

=(-1) [a ∙ (b x c)]

We can clearly see now that by switching rows we change the sign of our answer. But if I made two switches, then the answer would be (-1)(-1) times the original answer which would be the original answer. Therefore

a ∙ (b x c) = b ∙ (c x a)= c ∙ (a x b)

All of which involve two switches (794).

We used the TSP to find the volume of a parallelepiped earlier in this article, but one special condition that was not pointed out was that all three of the vectors must share a corner and they cannot be coplanar, or exist in the same plane. But what if they did? What would happen to the TSP? Well, if they were coplanar and in the same corner then they would all have to be the same vector, but possibly of different scalar lengths. Regardless, our matrix

| a₁ a₂ a₃ |

| b₁ b₂ b₃ |

| c₁ c₂ c₃ |

Will still equal a₁(b₂c₃ – b­₃c₂) - a₂(b₁c₃ – b­₃c₁) + a₃(b₁c₂ – b­₂c₁) but each component is just a scalar of the other. For our purposes, let’s say a = pb and c = fb. That is another way of showing how they are all related by different scalars. That will mean then that

a₁(b₂c₃ – b­₃c₂) - a₂(b₁c₃ – b­₃c₁) + a₃(b₁c₂ – b­₂c₁) = pb₁(b₂fb₃ – b­₃fb₂) - pb₂(b₁fb₃ – b­₃fb₁) + pb₃(b₁fb₂ – b­₂fb₁)

= pb₁(0) - pb₂(0) + pb₃(0)

= 0

Therefore, if the vectors are coplanar, then the TSP will equal 0 (795).

Larson, Ron, Robert Hostetler, and Bruce H. Edwards. Calculus: Early Transcendental Functions. Maidenhead: McGraw-Hill Education, 2007. Print. 794-5.