Try the partial quotient strategy to divide instead of confusion with long division
Division Anchor chart with multiple strategies
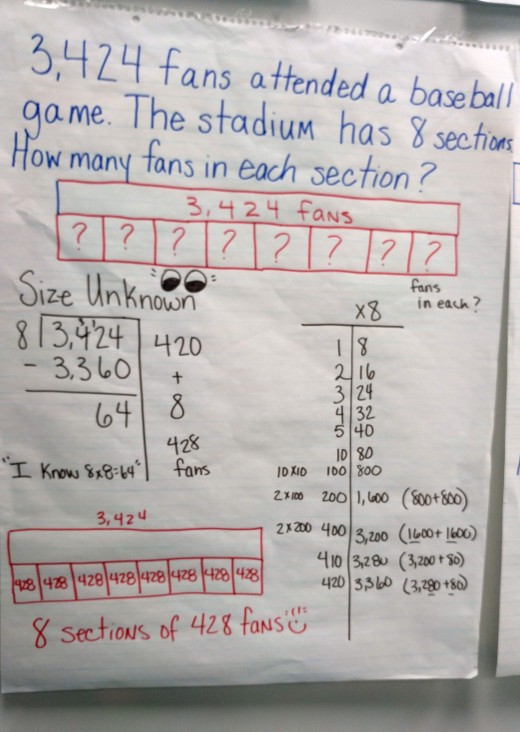
What is the partial quotient method?
In today's classroom, the NCTM and other mathematics associations are promoting researched based strategies to help students understand how to do math without feeling that they will just never understand math. Educators are teaching skills to facilitate a growth mindset when it comes to learning and applying math in everyday situations.
The partial quotient is a division strategy that allows students to multiply to divide using facts they know. They divide a part at a time until they get to zero or a remainder. Teachers are being encouraged to use this strategy because not only does it differentiate and allows kids to use what they know at their own level, but it makes it constantly reinforces the meaning of division.
Students are on a continuum of number sense growth and the more they practice the more they begin to see patterns. Remember that essentially you are multiplying to divide.The goal is to break the whole up until the whole number is gone or there is a small remainder.Students should think about how many digits are in the whole number. If I am dividing 245 by 5, I know that 245 has 3 digits so I first try to multiply 5x100, too big! So let's try 5x10=50 or 5x20=100 or we can do 5x40=200. I choose 5x 40=200, then subtract that from 245 and get 45. Now I can do 5x9=45. So 245 divided by 5= 40+9= 49 is the solution. Watch the following videos to see an example worked out step by step.
Watch as I guide through both the long division method and the partial quotient method.
Continuation
Division is repeated subtraction
From grade to grade students need to be able to use their prerequisites to build new understandings.Division is essentially repeated subtraction.When students get this fundamental fact, they can feel more comfortable understanding how division relates to multiplication. Since multiplication is repeated addition and division is its inverse, students need to be able to see how a whole can be broken up, separated, shared, partitioned into groups, or subtracted repeatedly.
Students can see division as repeated subtraction by using models through hands-on experiences.
Example: Take 20 buttons and divide it by 4. 20-4=16, 16-4=12, 12-4=8, 8-4=4, 4-4=0. Because 4 was taken away 5 times, 20 divide 4=5. When a student has this fundamental understanding they can divide larger numbers because the connection to subtraction gives them a starting point to grow from.
Solving Division Problems using bar models
Now in grade school kids are required not only to be able to compute solutions but to also be able to problem solve multiple to steps before using their computation skills. Using a bar model to visualize what is known and what is not known helps students to process the steps without getting confused. When students reading levels cause them to struggle through the text, slowing down to figure out what is known and what is unknown using a model, helps students stay on track throughout the problem solving process.
Remediate when students struggle with division concepts
If your child or students are not able to connect with division strategies take them back to the basics of multiplication. Students have to understand multiplicative thinking. To do so they have to see that groups can be repeated to represent a whole. when this understanding is solid then they can move on to breaking up the whole by subtracting from it repeatedly. This process along with hands-on activities, for students to see concrete models and make groups, will aid in building understanding or repair misunderstandings.
I would also suggest having students watch multiplication videos that incorporate music, my students learned a lot of their facts watching the Schoolhouse rock multiplication videos. Students should also do skip counting on a numberline, to see the jumps between intervals.
many free games and drills are available online to aid student practice to build their fluency. Furthermore, having kids chart their progress with division and creating growth goals will help them see their number sense increase and help to foster their ownership of their own learning.
How well did your teacher introduce Division?
How was your experience learning division in elementary?
Learn Multiplication with music!
More Resources
- How to create a 5 E Lesson Plan
The 5 E lesson plan format is described and explained. - Haiku poems lesson: Teaching poetry to 2nd grade stu...
Haiku poems are unique 17 sylable poems that can illustrate the meaning of something or express feelings in just a few descriptive words. This type of poem is a great poem to start teaching children poetry. In the second grade students are learning.. - Ordering Decimals on a numberline, and adding decima...
The lesson is for ordering decimals: provided with step by step procedures. Also an engaging game is included that will help students add decimals.

![Schoolhouse Rock: Multiplication Classroom Edition [Interactive DVD]](https://m.media-amazon.com/images/I/51tPqF2pxlL._SL160_.jpg)


