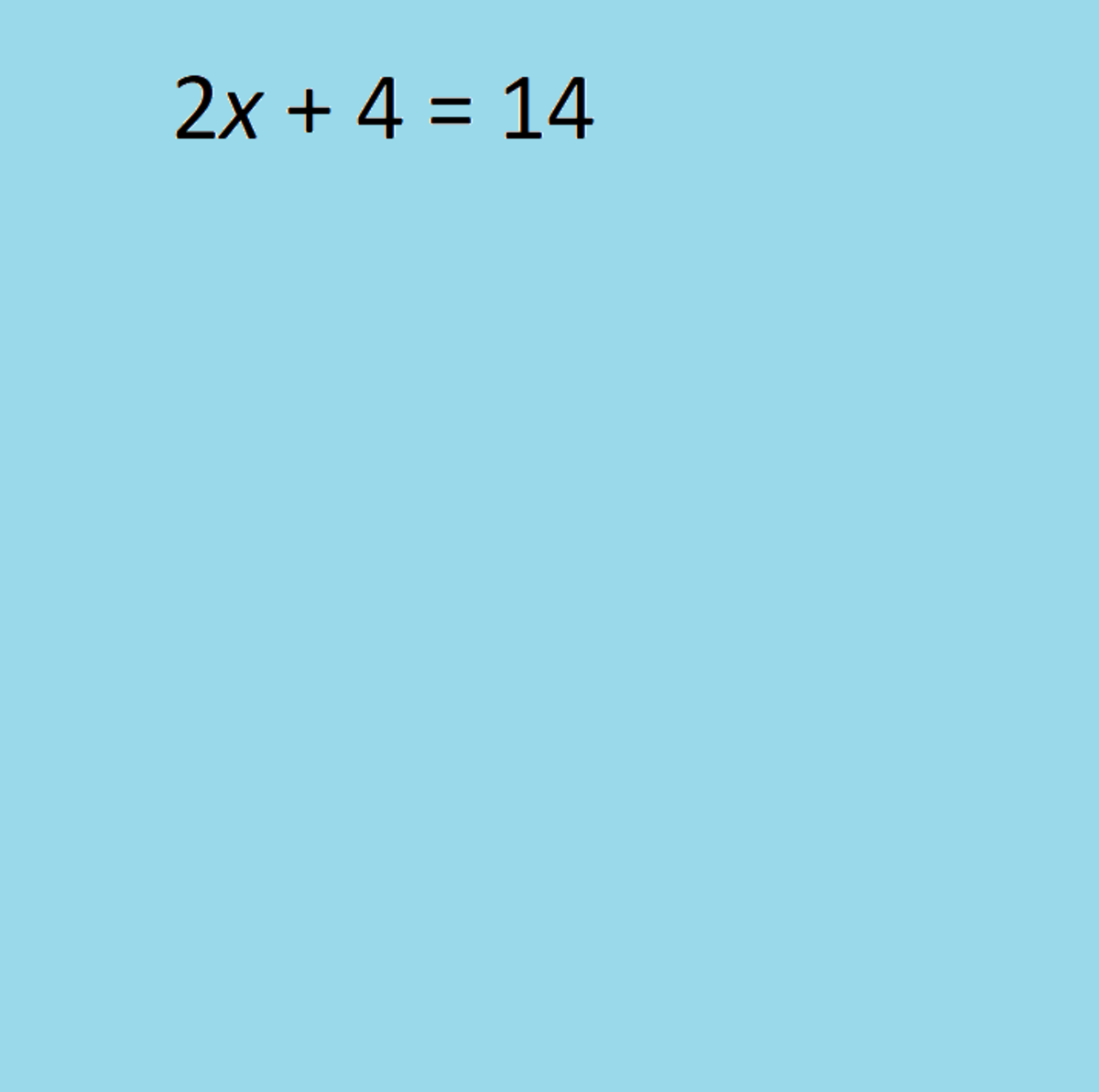How to Tutor Math Effectively - Techniques for Using the Textbook

When working with students, you’ve probably heard things like, “No matter how hard I study, I just can’t seem to do well on my math exams” or “I’m just not mathematically inclined; there’s nothing I can do to improve.” In these situations, a tutor will often take a “hammer approach,” or continuing to repeat the same drills and explanations over and over until they sink in. Unfortunately, this approach is generally ineffective and will only frustrate your student. Often, the student’s problem is simply not knowing how to study math correctly. As a tutor, guiding your students in techniques for effectively using their textbooks will help them build foundational skills for long-term success in math.

Help your students apply the following steps when using their math books, and you should see a noticeable difference in their learning. Help your student learn to…

• Preview the chapter by identifying key concepts, definitions, and methods.
• Don’t worry about understanding—your goal is to get a taste of what’s coming so that you’re mentally “warmed up” and familiar with some key terms before going into more detail.

• Read slowly and reread passages you don’t understand. Math textbooks are not repetitive—each word is important.
• (As a tutor, avoid the temptation to jump in and offer clarification and additional explanations. Instead, work on helping your students to develop the reading skills to comprehend the text on their own. For example, you could suggest something like, “This is a tricky concept. It’s ok if it doesn’t make sense right away. Try rereading the passage again, and this time break it apart into smaller pieces and follow along with the diagram for each part.” Your students will be much better served if you help them gain this valuable skill rather than just re-explaining the concept to them using the “hammer method.”)
• Pay particular attention to mathematical concepts. If you understand the concepts, you should be able to do any kind of problem, even those that are different from ones you have practiced. This is why you’ll often hear students complain that problems on the exam were different from what they studied in class—the instructor is testing your ability to apply the mathematical concepts to new situations, not your ability to memorize example problems.
• Read relevant sections before they’re introduced in class, not after. Then, you can use class time to clarify points of confusion. Try it—you may be surprised at how much more you’re able to learn during class time if you’ve previewed the material.

• Math concepts are learned by doing problems, not just by reading. As you read each sub-section in a chapter, copy down the example problems on a separate sheet of paper and attempt them on your own.
• Even if you get stuck on a problem and need to refer to the book’s solution, do the problem again on your own after reading the solution.

• Do the homework problems without looking up the answer until after completing the problem.
• When you get stuck, refer back to example problems for clues.A common mistake I see students make is looking up the answer while in the process of attempting a problem. You will learn the material better if you do the problems without first looking at the answer key. Plus, you won’t have this safety net when you take your exam.
• After you complete your homework for a given chapter, practice a few problems from earlier chapters. Math books typically group problems into chapters by concept, so continually reviewing earlier chapters ensures that you’re deeply learning these concepts.

At first, your students might be frustrated that you’re making them think so much on their own without just giving them “hints” or even the answer. When this happens, explain to them that you won’t be there to give them hints when they’re taking their exams. Instead, your goal is to give them the skills they need to succeed on their own and without your help. I promise you, your students will eventually thank you for it!

Reading a Math Textbook - Cynthia Arem, Ph.D., Pima Community College

Reading a Mathematics Text – Perla Myers, University of San Diego

How to Read a Math Textbook – Eric Neill, University of Houston – Victoria