Using and Understanding Statistical Averages: Mean, Median and Mode
When there is a large set of data, it is sometimes helpful to combine the data and extrapolate some measures of central tendency in order to help understand the data. These statistics help you understand large groups of data, and help you see trends over time.
The three main ways to statistically calculate large sets of data are mean, median and mode.
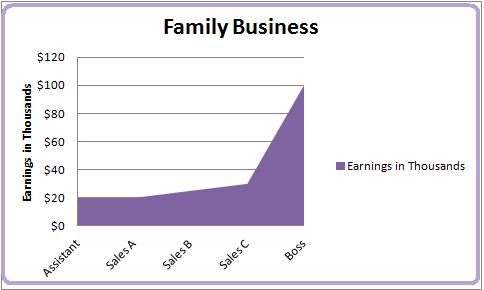
In this hub, we will calculate the mean, median and mode of this group of five numbers. There is a family that works in the office of a family business. They want to calculate these statistics to find their "average" earnings. Listed below are the salaries they earned last year.
- 20
- 20
- 30
- 25
- 100

When to Use Mean
The mean, or average, is the most frequently used statistic. It is used in most cases when a measure of central tendency is needed. It is only when this number cannot be calculated or provides a skewed result that you would switch to using a different statistic.
How to Calculate Mean
The mean is generally what you think of when you think of average. All of the numbers in the data are summed up, and divided by the number of figures that are in the data.
In this case, we add up all of the numbers.
20 + 20 + 30 + 25 + 100 = 195
We divide the total, 190, by the number of numbers, 5, to get 39.
20 + 20 + 30 + 25 + 100 = 195 ÷ 5 = 39
The mean of this group of numbers is 39.

When to Use Median
When there are numbers that are extremely high or extremely low on the data set, it is more helpful to use median, so that the outliers do not skew the results. In the case of this data, the 100 is very different from the others, and is making the mean look higher than what the majority of the data suggests. By using the median, the number is closer to what most of the people are making.
How to Calculate Median
The median is the middle number. In order to find it, you have to first organize your group of numbers in numerical order.
This group of numbers is now ordered.
20, 20, 25, 30, 100
In this case, the number in the middle is 25.
The median of this group of numbers is 25.
Please note that if there is an even number of numbers, then the median would be the mean of the two numbers in the middle. You would average the two numbers in the middle to obtain the median.

When to Use Mode
Mode is generally used when the data set is not a calculable set of numbers. If you ask the public to choose between politicians X Y or Z, you cannot calculate an average. The politician with the most number of votes would be the mode. Once you calculate the mode, you could say most people prefer politician X.
How to Calculate Mode
The mode is the number that has the highest frequency. In this group of numbers, since there are two 20s and only one of each of the other numbers, the mode of this group of numbers is 20.
Mean, Median and Mode
For purposes of a test, the information presented thus far is probably all you need to know about mean, median, and mode as measures of central tendency. However, these statistics are used frequently in real life, especially in the news about research studies and politics. It is important to understand how these numbers can be adjusted to correct flaws in the data or to confuse the public.
Real Life Application of Statistics
Statistics are helpful to get a general idea about the type of earnings that are generated by the family members. However, you have to be really careful about which numbers are being used and what they represent. Each of the scenarios listed below stand alone and will go back to the original numbers to avoid confusion.
Annualized Income
Since the income figures are from last year, some adjustments may need to be made to the numbers to reflect changes that will occur this year. For example, the person who earned $25 may have only worked part time last year, and is expecting $50 this year since she will be working full time. To get a more accurate representation of the average income, her salary should be adjusted to $50.
20 + 20 + 30 + 50 + 100 = 220 ÷ 5 = 44
The mean, or average, income for the family members who work in the business is expected to be $44,000 this year.
Household Income
While the $39,000 is a good average of what each of the members earned in the business, it may not be a good indication of the average household income if there are additional family members who worked elsewhere or were unemployed. Let's say there is an adult family member who is going to college and is not working. To accurately calculate the average each adult person is contributing to the household income, the student's earnings, or lack thereof, must be considered in the average.
0 + 20 + 20 + 30 + 25 + 100 = 195 ÷ 6 = 32.5
The mean, or average, household income is $32,500.
Expected Earnings
If a new family member wants to join the company, and is wondering about what types of earnings to expect, he would likely not want the boss's salary included in the average.
20 + 20 + 30 + 25 = 95 ÷ 4 = 23.75
The mean without the boss's salary is $23,750. This is a better indication of what kind of salary he can expect instead of $39,000.
The mean, or average, income of the workers in the family business, not including the boss, is $23,750.
Skewing the Statistics
If someone wants to entice a new family member wants to join the company, he may want to give her the average, even though she will likely to earn the minimum of $20 as a new employee.
If the new family member decides to join the company, she may likewise want to provide an inaccurate statistic to the boss try to garner a higher salary. She may tell the boss that the average salary is $39,000 to see if she can squeeze out a higher salary for himself. Even if the boss knows that the amount is skewed, it is possible that he doesn't take the time to calculate the accurate statistic, and wind up giving her more than she would have gotten otherwise.
Using Averages: Mean, Median, and Mode
Statistics are very useful in understanding large sets of data, and are especially helpful in seeing trends over time. However, since they can also be used to skew results, we must be very careful in properly understanding how they are calculated. When you are looking at averages to compare them over time, it is very important that they are calculated the same way every year. Also, when someone tells you something is an average, make sure you listen to the rest of the description. As we have seen, the average can change significantly depending on how it is being calculated.