How to Solve for Properties and Proofs of the Unit Vector for Calculus

In our discussion on vectors, it is oftentimes helpful to look at the components of that vector. We can see those individual parts when we write out a vector as a = <a₁, a₂, a­₃>. But what does each of these components mean? How can we find a way to look at the basic information that the parts mention? We must be careful not to get this confused with scalars, for those merely lengthen the vector or decrease it. We need a way to talk about the unit vector, or the most basic portion of the vector that conveys the information of it properly in a single length. But first, we need to examine how to find the length of any vector before we can talk about the basic material of that vector, and other fun properties from there.

When we take a vector and multiply it by a scalar, we are changing each of the components of the vector by the scalar. Whether the vector is increased or decreased in length and also changed in direction depends on the value of the scalar that is being applied to it. So how can we know how long that vector will be? Well, to find the length of a vector we need the magnitude, so for vector a that is increased by scalar c, the magnitude

||ca|| = [(ca₁)² + (ca₂)² + (ca₃)²]^0.5

= [c²a₁² + c²a₂² + c²a₃²]^0.5

= [c²(a₁² + a₂² + a₃²)]^0.5

Now, if I take the square-root of a number, then either the positive or negative value will work. A common example is (4)^0.5. Either 2 or -2 squared gives us 4. So (c²)^0.5 = c or –c. But since we want the length of the vector, we just care about the actual number and not the sign of it, so we need the absolute value of the square rooted number. So

[c²(a₁² + a₂² + a₃²)]^0.5 = |c|(a₁² + a₂² + a₃²)^0.5

=|c| ||a||

So if a vector is increased by a scalar, then the length of the vector is just the magnitude times the absolute value of the scalar, or ||ca|| = |c| ||a||. So we can see that the magnitude is a quantity we can solve for independent of the scalar. Does this help us in our discussion of the basic vector components? (Larson 766)

Since the magnitude itself is independent of the scalar we apply to it, we can use that to find the unit vector, or the basic vector whose magnitude equals one. This is important because we will gain the ability to talk about the components of the vector in the x, y, and z directions and how much of the vector is in each of those directions. The goal of the unit vector is to have a magnitude (length) of 1. To achieve this, we need to normalize our vector a, or divide it by the length of the vector. Hence, the unit vector of a is a / ||a||. So how do we know that this new unit vector we have created will have a length of 1? Well, so long as a is not the zero vector, the magnitude of the unit vector is || a / ||a|| ||. But notice that

|| a / ||a|| || = |(1/||a||)|* (||a||)

Because from before, we know that any scalar does not change the magnitude of the vector, and the |(1/||a||) is just a scalar. Also, since the result of any absolute value is a positive number,

|(1/||a||)|* (||a||) = (1/||a||)* (||a||)

But now I have the same number on top and the same number in the denominator, so

(1/||a||)* (||a||) = 1.

So, by normalizing any vector, we will create a unit vector in the direction of a (766).

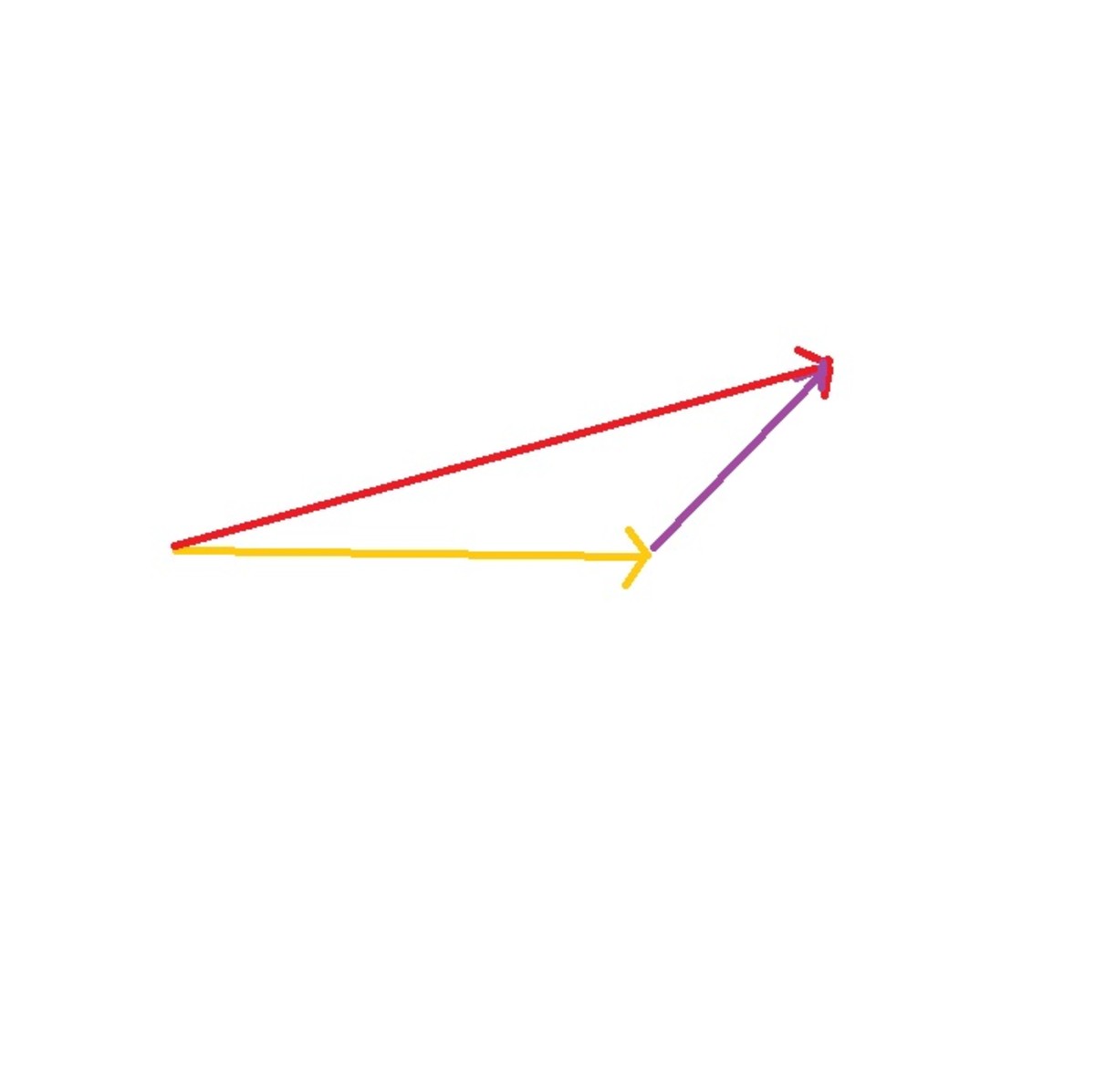
Notice that if vector a = <a₁, a₂, a₃>, we can split this up as

<a₁, a₂, a₃> = <a₁, 0, 0> +<0, a₂, 0> + <0, 0, a₃>

Because of vector addition. Also notice that we can rewrite the vector as

<a₁, 0, 0> +<0, a₂, 0> + <0, 0, a₃> = a₁<1, 0, 0> + a₂<0, 1, 0> + a₃<0, 0 ,1>

Because of scalar multiplication. But notice that I now have a bunch of vectors that are 1.
These are all special unit vectors because of the direction they point in. We use the letters i, j, and k to represent these unit vectors. The unit vector i = <1, 0, 0>, j = <0, 1, 0>, and k = <0, 0, 1>. So we can rewrite

a = a₁<1, 0, 0> + a₂<0, 1, 0> + a₃<0, 0 ,1> = a₁i + a₂j + a₃k

The i component tells us how much of the vector is in the x-direction, the j component tells us the amount in the y-direction, and the k component tells us the amount in the z-direction. With these components known, it becomes easier to employ the properties of vectors and also give us a way to talk about how a vector operates in the x-y-z space, all with the basic components of each vector (767).

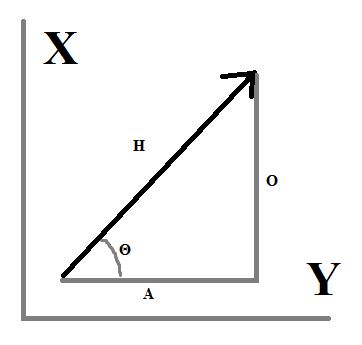
So what if I did not know that a = <a₁, a₂, a₃> ? How could I get the x, y , and z components? Let’s look at an x-y example. If you know the number of degrees that the vector is above/below an axis, you can use SOH-CAH-TOA. In this case, you know that the hypotenuse is the length of the vector ||a|| but what would that opposite side, or the y-component, be? Sin Θ = O/H = O/||a|| so that opposite side will equal ||a|| Sin Θ. Similarly the adjacent side, or the x-component, will equal ||a|| Cos Θ. Therefore, for any vector that is Θ above the x-axis,

a = ||a|| Cos Θ i + ||a|| Sin Θ j (768).

Thanks for reading! Be sure to check out my other hubs on calculus proofs for even more insight into how it is done.

Larson, Ron, Robert Hostetler, and Bruce H. Edwards. Calculus: Early Transcendental Functions. Maidenhead: McGraw-Hill Education, 2007. Print. 766-8.