Relative frequency. Can someone explain relative frequency is an easy way?

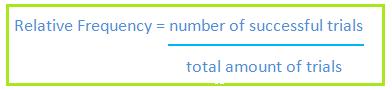
Relative frequency is basically the experimental probability. Imagine that you toss a coin 100 times and you get a head 42 times, then the relative frequency for tossing a head is 42/100 = 21/50. You can use the formula shown below to work out the relative frequency:

Relative Frequency = (number of successful trials)/(total amount of trials)

As you increase the amount of trials in the experiment the relative frequency becomes closer to the real probability. So in the example of tossing a coin, the relative frequency of tossing a head will get closer to the real probability of ½ as you increase the amount of coin tosses. If the relative frequency didn’t get closer to the real probability as you increased the amount of trials then the coin would be biased (not fair).

Let’s take a look at another example:

Ian is conducting an experiment to see if he has a fair dice. He records the amount of times he rolls a 6 after 10 rolls, 20 rolls, 30 rolls, 40 rolls and 50 rolls. Work out the relative frequency of rolling a 6 after 10 rolls, 20 rolls, 30 rolls, 40 rolls and 50 rolls. Use these results to decide if the dice is fair or not.

Amount of 6’s from 10 tosses = 1

Amount of 6’s from 20 tosses = 3

Amount of 6’s from 30 tosses = 3

Amount of 6’s from 40 tosses = 4

Amount of 6’s from 50 tosses = 4

To begin with use the above formula to work out the relative frequency at the end of each stage:

Relative frequency after 10 tosses = 1/10 = 0.1

Relative frequency after 20 tosses = 3/20 = 0.15

Relative frequency after 30 tosses = 3/30 = 0.1

Relative frequency after 40 tosses = 4/40 = 0.1

Relative frequency after 50 tosses = 4/50 = 0.08

The real probability of rolling a 6 on a dice is 1/6 (or 0.17). As you can see as the amount of rolls increases the relative frequency seems to be diverging from 0.17. So you would have to include that the dice is biased, so there is smaller probability of rolling a 6 on Ian’s dice than a fair dice.

Example 2

Beth has a 5 sided spinner with the numbers 1,2,3,4 and 5. She spins the spinner 500 times and records the amount of times she gets each number:

Amount of 1’s = 102

Amount of 2’s = 99

Amount of 3’s = 98

Amount of 4’s = 100

Amount of 5’s = 101

Is the spinner fair?

If the spinner is fair then the relative frequency for each number should be about 0.2, since the real probability of spinning each number should be 1/5:

Relative frequency for a 1 = 102/500 = 0.204

Relative frequency for a 2 = 99/500 = 0.198

Relative frequency for a 3 = 98/500 = 0.196

Relative frequency for a 4 = 100/500 = 0.2

Relative frequency for a 5 = 101/500 = 0.202

As you can see the relative frequency for spinning each number is very closer to 0.2. Since the amount of spins was large then you would conclude that the spinner is fair.