What do all those Maths words mean?

We all understand that your children could be struggling with their maths homework. We have to think, are they struggling with the maths or are they struggling with the language?
Expand, evaluate, solve, simplify, factorise, sum, product…the list is endless. With a few reminders and triggers for what the words mean then Maths will become more accessible.
When I ask:
“What do we need to do when we see the word factorise?”
My pupils will always respond:
“Put the brackets in!”
Factorise and brackets are embedded and connected in my pupil’s minds.
Now for my disclaimer, some of this may not be mathematically correct (as in how we would teach) but it is a way that over time has helped pupils to remember and stopped the cry “I can’t do Maths!”

Number based words
Sum, total, difference, product, integer are all words that stop pupils in their tracks.
I will start with the one that always makes me smile, because I will always be asked “intega? what is an intega?” Obviously, my first reaction is to correct them on the pronunciation “integer” then go on to explain.
An integer is any whole number either positive or negative.
The next few words
Sum – add
Find the sum of the first three consecutive numbers…and there’s my next problem consecutive, things that follow on such as 1, 2, 3 or 7, 8, 9 or 2, 4, 6 (for consecutive even numbers)
The sum of the first three consecutive numbers is 6 because 1 + 2 + 3 = 6
Difference – subtract
The temperature was 9 degrees and dropped to 3 degrees what is the difference in temperature?
9 – 3 = 6 the temperature difference is 6 degrees
Total – add
What is the total amount spent if you buy a chocolate bar for 60p and a drink for £1.30?
60p + 130p = 0.6 + 1.30 (I hope you can see here, I have changed the pounds into pence or vice versa to complete the calculation)
Total amount spent would be 190p or £1.90
Lots of – multiply, times
6 lots of 20p is £1.20
See the word OF you always multiply (especially with fractions 2/3 of 6, ¼ of a ½)
Product – multiply, times
This word would normally come up with prime factors which is further down the page…
The product of 6 and 3 is 18.
6 x 3 =18
Multiple
Sounds like multiply/multiplication...a multiple is the result of multiplying.
The 5th multiple of 7 is 7 x 5 = 35
35 is a multiple of 5 and 7
Factor
If you've addressed MULTIPLE then factor becomes easier. Factor is a number that will divide into another number. Factors usually come in pairs. For example:
Factors of 12 (always remember 1 x the number..)
1 x 12
2 x 6
3 x 4
Factors of 12 are 1, 2, 3, 4, 6 and 12
Collecting coins to find our how much money you have, is similar to collecting like terms in algebra

Now for Algebra…
Constant
This is a number on it's own.
3x + 2
2 is the constant
Coefficient
The number generally in front of the letter in an algebraic term. It tells you how many of the term you have.
3c means c + c + c = 3 lots of c or 3 x c
5x means x + x + x + x + x
6 apples means you have 6 apples, the number is the coefficient - how many you have
Variable
The letter is a variable. It can change depending on what the coefficients and constants are asking.
6x + 2 = 20 when x = 3
BUT
6x + 2 = 32 when x = 5
Like terms
The things that have the same variable. Remember the coefficient tells you how many you have.
6x and 5x are like terms
3xy and 2yx are like terms
5adg and 7adf are NOT like terms
Collect together like terms and simplify
If you are sorting a pot of change you would collect together all the 1p, 2p, 5p, 10p etc and then find out the total amounts of each coins. You might stack the coins in piles and then add them like the photo above!
It's the same in algebra you look for the terms that are the same and add or subtract depending on the operator in front of the term.
Look:
5x + 2y + 3x + 2x2 - y + 4x2 - 3
Read the expression (oh no another maths word there! Keep reading to find out what it means) and look for things that look are the same (the same coins...)
+ 5x + 3x
+ 2y - y
+ 2x2 + 4x2
- 3
Now total those coins:
8x + y + 6x2 - 3
Expression, equation, identity and what does equal really mean?
Simplify an expression...
Simplify - collect together like terms (see above)
Expression - groups of symbols and numbers grouped together (it doesn't have an equals sign)
3a + 2b - 3c
Equation - something that can be solved (another word there!) it has an equals sign
3x + 2 = 8
3x = 6
x = 2
Solve - find the value of the variable (the letter(s)) in the equation
in the example above we found the value of x to solve the equation.
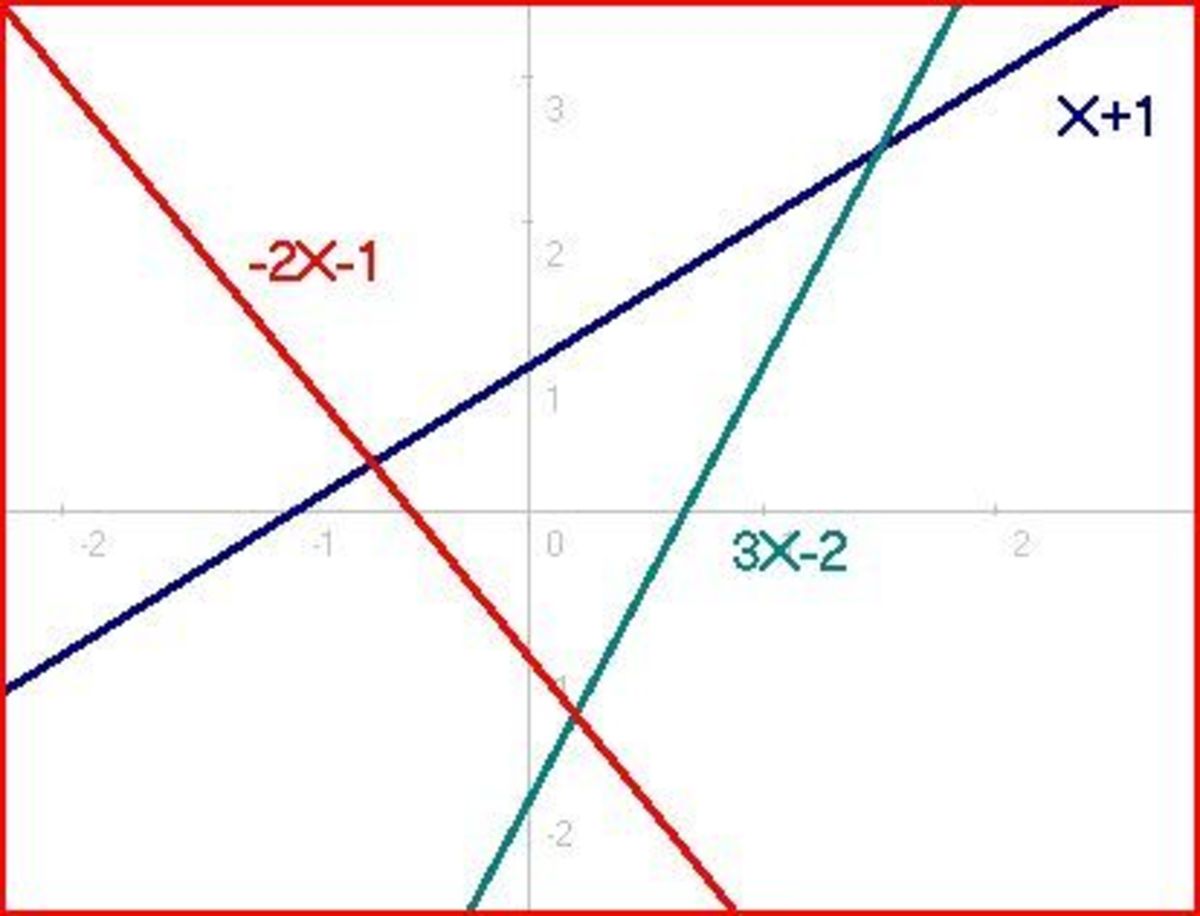
Identity
This is a word that is becoming used more often. It tells you that it is true regardless of the values chosen. (see the diagram below)
Equals sign
Yes I am about to shout
THE EQUALS SIGN DOES NOT TELL YOU THE ANSWER, THE EQUALS SIGN TELLS YOU THE LEFT SIDE IS EQUAL (the same as) THE RIGHT SIDE
3 + 4 = 5 + 2
60 SECONDS = 1 MINUTE
Identity

Algebra questions
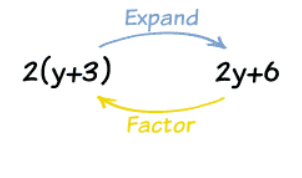
Sometimes you will be asked to expand or factorise. These are two distinct questions that you will come across and if you know they involve brackets then the maths will be easier to access.
EXPAND - remove the bracket
FACTORISE - put into brackets
Obviously, there is more maths behind this. But, if your child knows which is remove and which is put in then I am sure they will be able to access the question from their lesson. The example below may help.
Primes, squares, surds, linear, quadratic...the list is endless
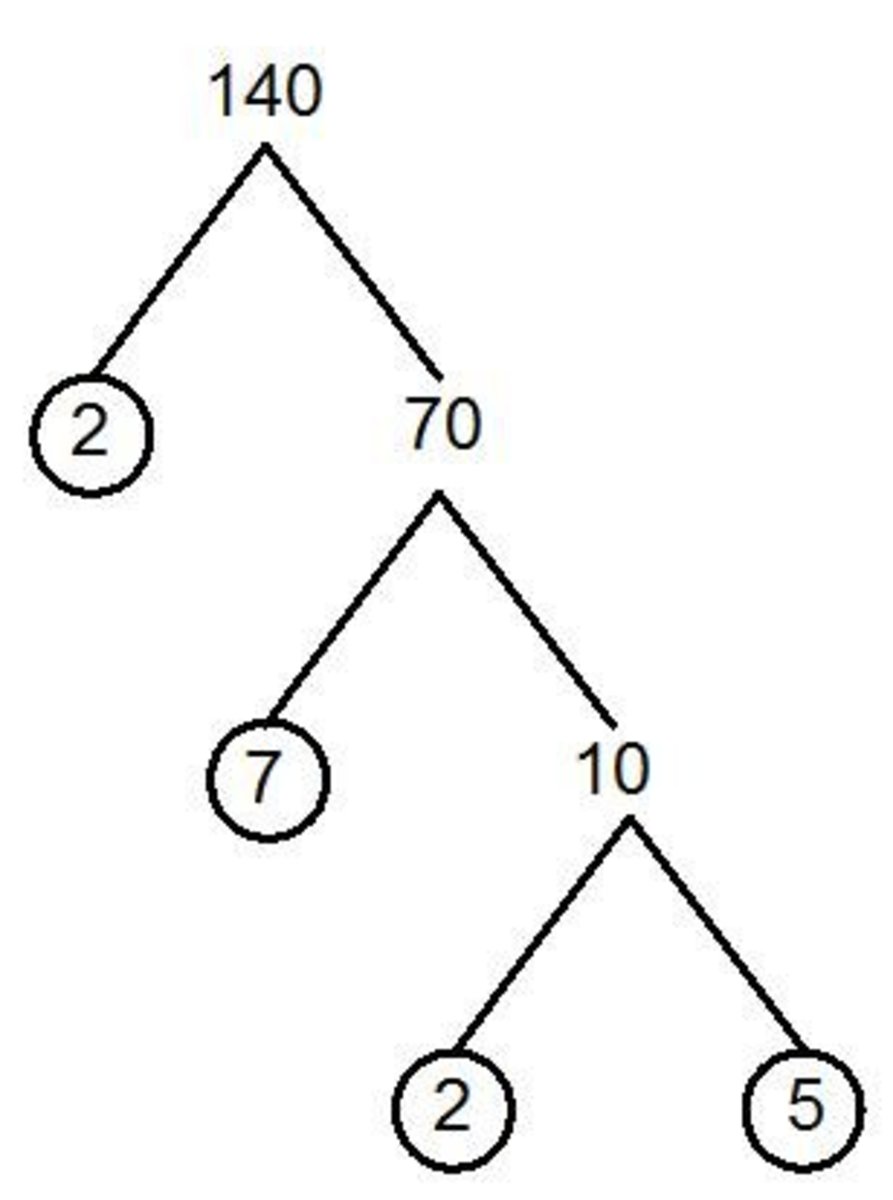
Earlier I mentioned prime factors. Now, these I find amazing! Any number can be made by multiplying together different combinations of prime numbers!
First we need to know what a prime number is. A prime number only has two factors, they are 1 and the number itself. Prime numbers below 50 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 (some of you might be asking where is 1, well 1 only has one factor (it's a square number)
Prime Factors
36 as a product of primes would be 2 x 2 x 3 x 3
Remember- product is multiply, primes numbers with only two factors
Square Numbers
If I multiply a number or letter by itself the result is a square
32 = 3 x 3 = 9
h2 = h x h = h2
Square root
The opposite of square numbers - which number do you multiply by itself to get the given number
Surds
This is a funny word - always makes me smile and say turd...In fact when I teach rationalising the denominator I will often say "we don't want any surds on our bottom"
But a surd is a number that can't be simplified to remove a square root
I could continue but the words are endless.
Final thoughts..
If you understand the words the maths becomes easier. Don't be afraid of using maths words when you speak with your children. Interchange them, if you're testing their times tables 6 times 3, 4 multiplied by 5, the product of 2 and 8.