What is 2 Pi radians in degrees? How to change radians into degrees (angular measure).
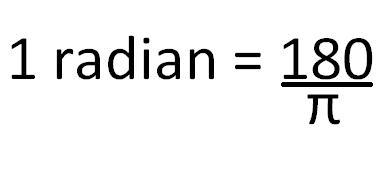
Radians are another type of angular measure. One radian is equivalent to 180/π degrees (or 57.3⁰). Certain calculations are much easier to work out in radians, such as, calculating the area and perimeter of a sector. Also make sure that you switch your calculator into radians if you are using any of the trigonometric functions, such as, cosine, sine, or tangent.
In order to change an angle from radians into degrees, all you need to do is multiply the angle in degrees by 180/π.
Example 1
What is 3 radians in degrees?
All you need to do is multiply by 180/π
3 × (180/π)
= 540/π
= 172⁰ rounded to 3 significant figures.
Example 2
What is π/3 radians in degrees?
Like example 1, all you need to do is multiply by 180/π.
(π/3) × (180/π)
= (180π/3π)
= 180/3 (the Pi on the numerator and denominator get cancelled out)
= 60⁰
Example 3
What is π/5 radians in degrees?
Again, multiply the radian angle by 180/π
(π/5) × (180/π)
= (180π/5π)
= 36⁰ (the Pi on the numerator and denominator get cancelled out)
Example 4
What is 2π radians in degrees?
Again, multiply the radian angle by 180/π
2π × (180/π)
= (360π/π)
= 360⁰ (the Pi on the numerator and denominator get cancelled out)
Example 5
What is (3π/2) in degrees?
Just like examples 1 to 4, just multiply the radian measure by 180/π
(3π/2) × (180/π)
= (540π/2π)
= 270⁰ (the Pi on the numerator and denominator get cancelled out)
So converting angles from radians into degrees is actually quite easy to do. All you need to do is multiply the angle in radians by 180/π.




