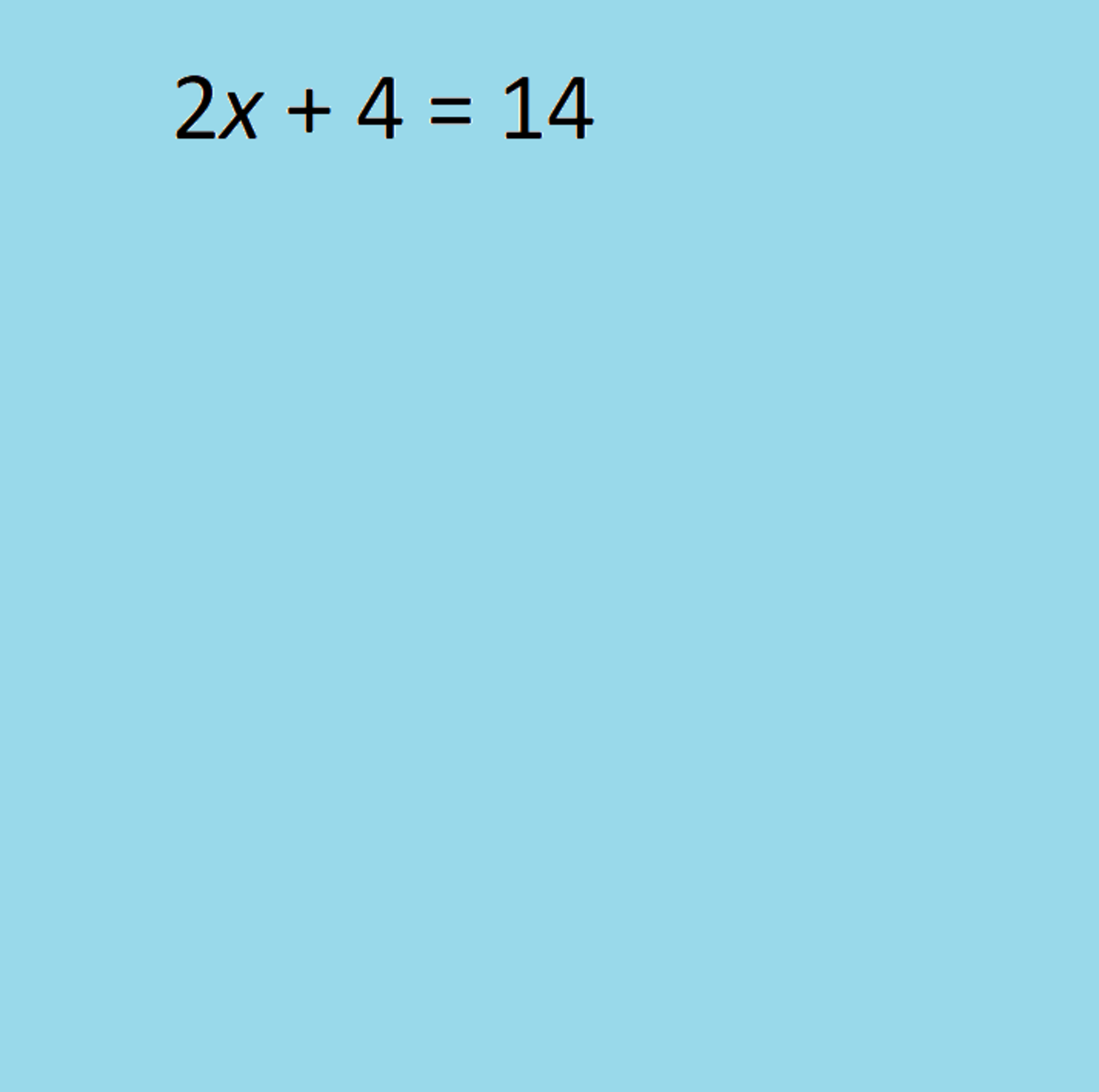What is the Quadratic Formula?
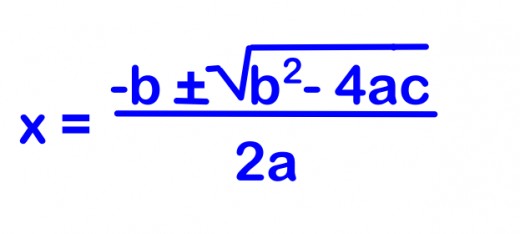
The Basic of the Quadratic
The quadratic formula is an essential part of algebra and understanding how to solve problem with a specif form.
ax2 + bx + c = 0 - this form of equation can be solved using the quadratic equation
Every quadratic equation has two solutions known as roots. Quadratic equations can also be solved using graphing techniques or factoring. The method shown here is using the quadratic equation in order to find the roots.
The Quadratic Equation
What is the point?
The goal is to find x. X is the unknown variable in the polynomial equation.
Why can't "a" be 0?
Remember a can not equal 0 - otherwise this equation won't work. If a = 0 than it isn't the correct format because a times any variable will always be 0 so the equation would not have a power of 2. and would only be bx +c
The Quadratic Equation
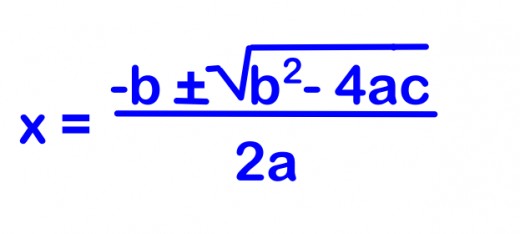
EXAMPLES of the Quadratic Equation
The first thing we need are defined variable for a, b, & c.
For this example a=2, b=4, & c=-6
I am using this numbers because they will work out to a nice even number
You are looking for two roots of the quadratic. Remember the sign that says plus or minus that is because you will need to do the last part of the equation twice - once in addition and once in subtraction.
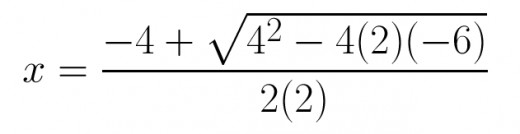
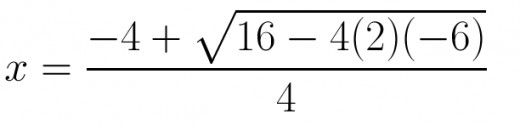
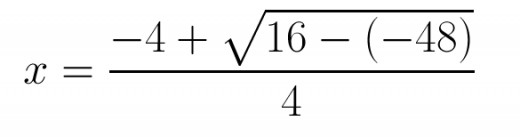
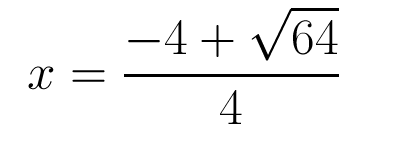
Solving for the Frist root with addtion
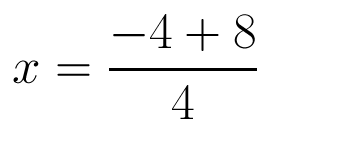
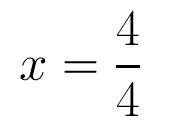
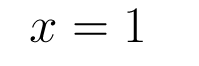
Solving the first root
In order to solve the first root we are going to use addition in the equation
Solving the Second Root
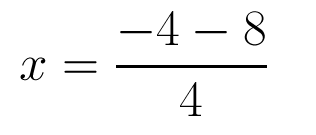
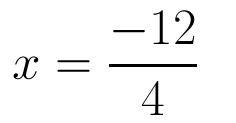
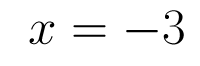
Solving the second root
In order to find the second root we will go back to where we left off before we solving the first root and use subtraction instead of addition.
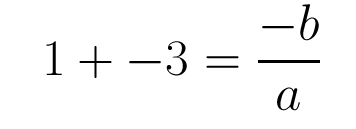
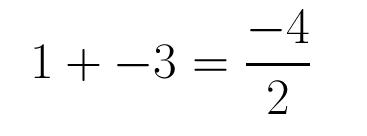
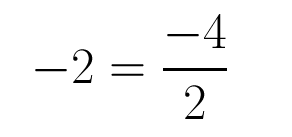
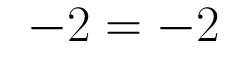
How to Check Your Roots
In order to check your anser you must check your roots. If it is correct the sum of the roots should be equal to -b/a