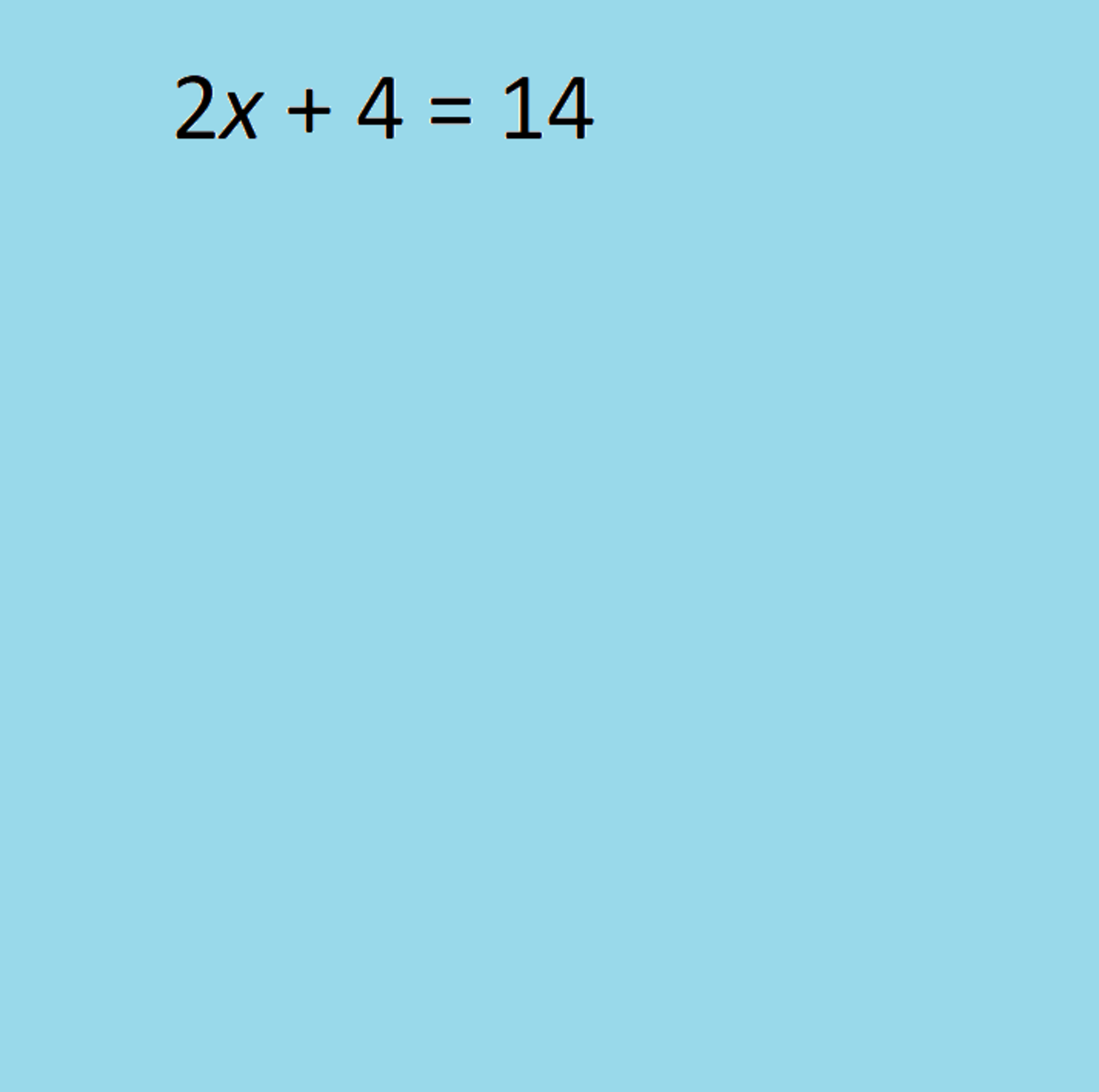Work Problems in Mathematics
Work problems usually involve the time for two or more persons or machines to complete the same job given the rate that they can work.
There is only one equation you need to remember for work problems.
Work = Rate x Time
Notes on using the formula:
1. The formula assumes that the rate of work is constant.
2. Work, in most cases, is usually set to be equal to 1. It follows that rate = 1/time.
3. If work involves several number of persons (manpower), the formula becomes work = manpower x rate x time. The unit of work becomes man-hours or man-days.
Example #1
Problem: Deo can do a job in one hour, Jin can do it in two hours, and Kay can do it in three hours. How long will it take them to do the job working together?
Solution:
Their rates are
Deo: 1 work/1 hour = 1 work/hour
Jin: 1 work/2 hours = 1/2 work/hour
Kay: 1 work/3 hours = 1/3 work/hour
Let t be the time each of them are working together to finish 1 work. Since work = rate x time, the part of 1 work that each of them will finish are
Deo: (1)(t) = t
Jin: (1/2)(t) = t/2
Kay: (1/3)(t) = t/3
The total work that they will finish is 1 work. Hence
t + t/2 + t/3 = 1
11t/6 = 1
[t = 6/11 hours = 0.5455 hours]
Example #2
Problem: Twenty men can finish a job in 30 days. Twenty-five men started the job. After 20 days, 10 men quitted. Find the total number of days it took them to finish the job.
Solution:
The total work to be done is (20 man)(30 days) = 600 man-days.
However, 25 men started the job in 20 days, and (after 10 men quitted) the remaining 25 - 10 = 15 men worked for t days until the entire work is finished. The total work in this case is 25(20) + 15t = 15t + 500 man-days.
Since the two are just the same work, we equate the two:
15t + 500 = 600
15t = 100
t = 20/3 days
Therefore, the entire work can be finished in 20 + t = 20 + 20/3 = [80/3 days = 26.6667 days].
Example #3
Problem: JR and RJ working together can finish painting a house in 6 days. JR working alone can finish it in 5 days less than RJ. How long will it take each of them to finish the work alone?
Solution:
Let t be the time required by RJ to finish the job alone. Then (t - 5) be the time required by JR to finish the job alone.
Thus, their rates are: JR = 1/(t - 5) work/day, RJ = 1/t work/day.
Since they finished the work together in 6 days, their share of works using work = rate x time are: JR = 6/(t - 5), RJ = 6/t. The total work is 1 work, hence
6/(t - 5) + 6/t = 1
6t + 6(t - 5) = t(t - 5)
6t + 6t - 30 = t^2 - 5t
0 = t^2 - 17t + 30
0 = (t - 2)(t - 15)
t = 2 days or 15 days (RJ's time)
t - 5 = -3 days or 10 days (JR's time)
We discard t = 2 days, since t - 5 = -3 days (not allowed). Hence, RJ = [15 days], while JR = [10 days].