You Must Leave Earth to Lose Weight

In the 17^th century, an incident, perhaps apocryphal, has it that the English scientist Sir Isaac Newton was inspired to contemplate why objects fall to the ground after experiencing an apple falling on his head.

Let’s relate Sir Isaac Newton’s notion of gravity to the following scenario.

A 10 kilogram (22 pound) steel sphere and a 3 gram (0.1 ounce) ping pong ball are dropped from a skyscraper. Which will hit the ground first?

You are correct if you said the steel sphere will reach the ground first, but not because it is the heavier of the two objects. It is because Earth’s gravity produces a gravitational acceleration, g, on every falling object that has magnitude of approximately 9.8 metres per second per second (or 9.8 m/s²). This means that each second, the speed of the falling object increases by 9.8 m/s.

The value of g changes slightly. Generally, the higher above the Earth’s surface you are, the less gravitational acceleration you will experience.

Gravitational acceleration is also independent of weight.

But why, then, does the steel ball reach the ground first? It is because external forces diminish the effects of the gravitational acceleration. For instance, air resistance is greater for the ping pong ball than for the sphere, so gravitational acceleration will be less.

In the absence of external forces such as friction and air resistance, objects will take the same amount of time to reach the ground. This was clearly demonstrated in 1971 by Commander David Scott of the Apollo 15 moon mission. He dropped a hammer and a feather, and because there is no air resistance or other force, both objects reached the ground at the same time.

What we refer to as weight is the size of the force, F, exerted on the object by Earth’s gravitational acceleration. Close to the Earth’s surface, this is found using the formula F = m × g, where g is 9.8 m/s² and m is the mass. For a 1 kg mass, F is 1 × 9.8 = 9.8 Newtons.

Note the unit of force, Newtons, in honour of Sir Isaac Newton. Also note the distinction between mass and weight. Mass does not change, but weight does, depending on the value of the gravitational acceleration.

Since m is constant, F (the weight) will change only if g changes. Thus, a flag of weight 2 kg at the base camp of Mount Everest may well weigh only 1.8 kg at the summit.

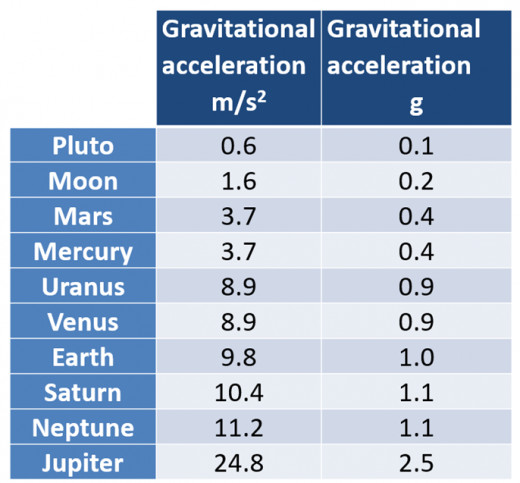
The gravity, and hence the gravitational acceleration, on other planets and on our moon is not the same as what we have on Earth. The table below shows the approximate gravitational accelerations existing on other planets. It is expressed in terms of m/s² and also in terms of the Earth’s gravitational acceleration, g = 9.8 m/s².

For example, the gravitational acceleration on Jupiter is 24.8 m/s², which is 2.5g, or 2.5 times greater than Earth’s gravitational acceleration.

From the table above, the moon’s gravitational acceleration is 1.6 m/s² or approximately g/6 m/s², which is about 1/6 of Earth’s gravitational acceleration. This explains why astronauts on the moon’s surface can jump higher than they would be able to jump on Earth. There is less gravitational force exerted on them.

On the other hand, an astronaut on Jupiter will experience an acceleration of about 2.5g m/s², hence jumping in the air will be severely restricted in terms of height reached.

On the moon, the gravitational force on a person of mass 72 kg means the weight will be approximately 1/6 their weight on Earth, or just 12 kg!

Is this equivalent to dieting taken to its extreme?

We have determined that the lower the gravitational acceleration, the higher you can jump, but let’s be more specific by performing some calculations and making comparisons.

The world high jump record is 2.45 m, set by Javier Sotomayor of Cuba in 1993. How high would he have been able to jump on another planet?

An equation of kinematics (the study of motion of a moving object) is 2as = v² – u². Here a is the gravitational acceleration, v is the final speed, u is the initial speed and s is the distance travelled. First, let’s find the speed at which Javier leaves the ground.

Javier’s maximum speed is u = 0 m/s (at the highest point). His distance covered is s = 2.45 m and the gravitational acceleration is a = -9.8 m/s². (Negative, because it is acting opposite to the direction of motion).

We substitute these values in the formula 2as = v² – u² to obtain u² = 48.02. Hence u is approximately 6.92 m/s.

Our formula 2as = v² – u² now becomes -2as = 0² – 48.02 or s = 24.01/a.

This will give the maximum height, s, for different values of the gravitational acceleration, a.

The maximum height for different planets is shown in the following table.

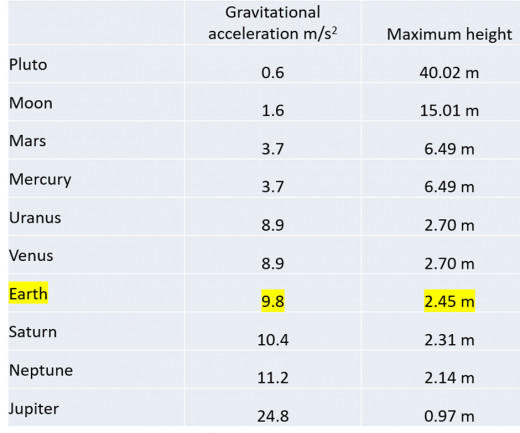
Notice that if Javier made his jump on Pluto, he would reach a maximum height of about 40 m, equivalent to the height of an 8 storey building! On the other hand, it would be unwise to jump on Jupiter because he would get to no more than 97 cm off the ground.

If you want to break high jump records or to instantly lose weight, go to Pluto. So book your interplanetary ticket now to avoid the holiday rush!