Addition and Subtraction (Curious Concepts Precalculus 1.2)
Self-explain Learning Technique
Self-explain Learning Technique helps people to better comprehend, and remember any thing they want to learn. It my sound strange, but it is many times more effective then re-reading. To use this technique, give short answers to the prompted questions. Incorporate previous knowledge-and-life experience into your answer will make this learning technique more effective. On average it improves learning by over 2.5 standard deviations; the difference between a C student and an A student.
What is the largest number you can count by?
Addition
Addition is the core operation in math. It is the base from which all other math operations grow. The premise of addition is simple: If we are holding up one finger and then hold up another, how many fingers are we making a rude gesture with? We count by adding 1 to the previous number starting with 1. We can count by 2's, by adding 2 to every previous number starting with 2.
Adding Smaller Numbers
You can add any set of numbers in any grouping and in any order you want. The communicative and associative properties allow us to do this and by using them we can make addition problems simpler to solve. If we are given a long string of numbers we can add them in groups and then add the groups together. This is called “chunking” because we are making one big problem into a set of smaller ones, or chunks.
Example:
5+6+2+3+9+14+11 = (5+6)+(2+3)+(9+!4)+11 = 11+5+23+11 = (11+5)+(23+11) = 16+33 = 49
We can also add them in any order. If we can make them into groups that are easier to add.
Example:
5+3+9+4+2+1+6 = (5+2+3)+(9+1)+(4+6) = 10+10+10 = 30
Adding Large Numbers
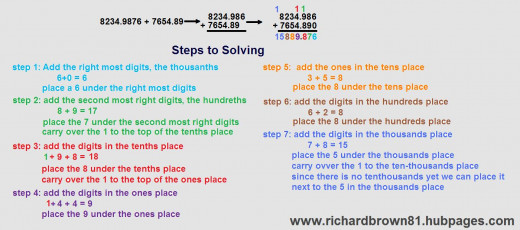
We can use the same principle to break down complete numbers. This makes it possible to turn the addition of large numbers a set of smaller addition problems. To make this a simple stream lined process, we place the numbers that I need to add on top of one another. The two numbers are aligned with each other, so that the ones places are on top of one another. If there is decimal places, then we add 0's, so that they have just as many digit places in all the numbers to be added. We then add the single digits, starting with the right. If the sub-total is more then one digit, we place the right-most digit of it under my addition line and carry over the left digit to the top of the next place.
Self-Expain Learing Technique
How could you know, how much money is in your wallet with out looking?
Subtraction
Subtraction is how to undo addition. This is because of a very special number: 0
a+0 = a
This holds true for all real numbers.
Every real number a has a negative: -a. This satisfies: a+(-a) = 0.
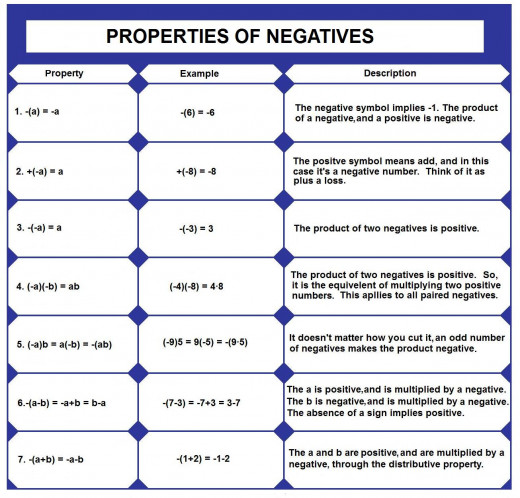
Subtraction is the operation used to undo addition. To subtract a number, we simply place a negative sign in front of it. So, a-b = a+(-b) by definition.
We can also apply the communicative and associative properties to subtraction. By definition subtraction is adding a negative number. We can subtract in any order, and in any grouping; and still get the same answer. We just have to be careful about keeping the negative values negative, and the positive values positive.
Example:
3-4-8-1-5-3-7 = 3+(-4-8-1-5-3-7) = 3+(-3-7)+(-4-1-5)-8 = 3+(-10)+(-10)-8 = 3+(-28) = -25
Again, because subtraction is adding a negative number; we can break down larger numbers into groups of smaller number, so that problems are easier to solve.
Example:
-27-28-31-26 = (-25-2)+(-25-3)+(-25-6)+(-25-1) = -25-2-25-3-25-6-25-1 = (-25-25-25-25)+(-2-3-6-1) = -100-12 = -112

Self-expain Learing Technique
How is it that if you multiply by a negative number, the answer is negative?
Properties of Negatives
Subtraction is simply adding a negative number, nothing more. Real Numbers have the following properties involving negatives.