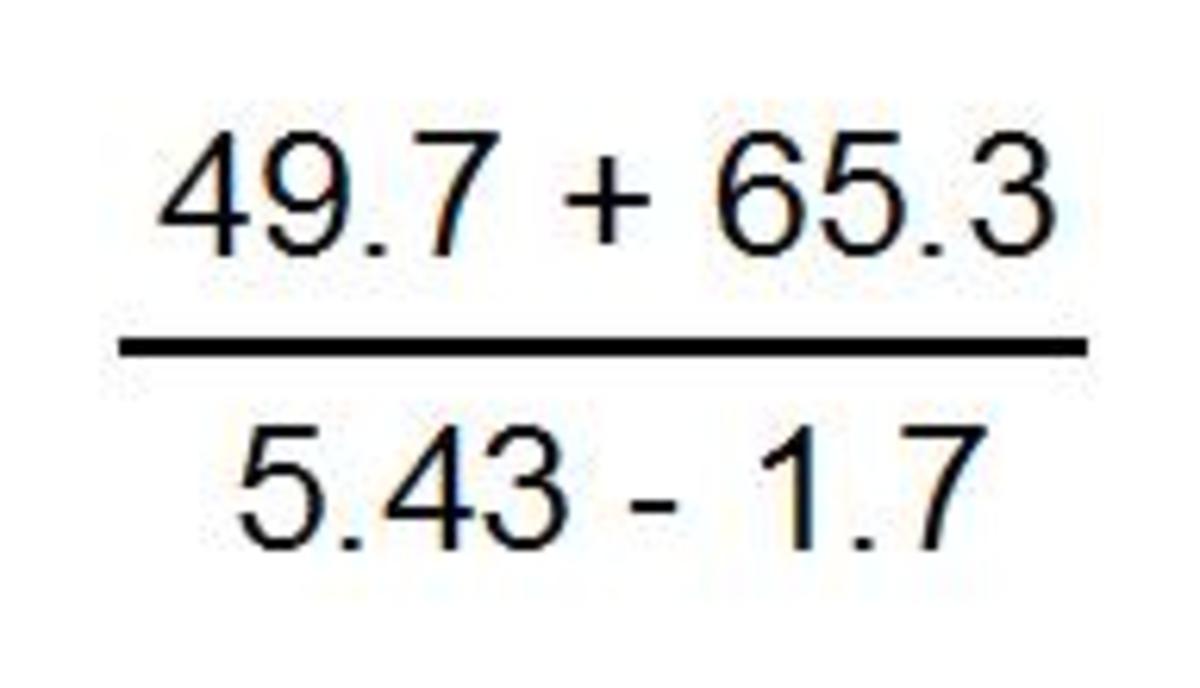Algebra: Exponents

Explaining Exponents
In the years I've been tutoring, I have noticed that many people find the concepts of exponents to be a very daunting one. But exponents are really only an easier, more understandable way of expressing larger, more cumbersome numbers. I hope you feel less intimidating after reading this.
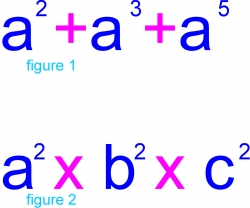
Firstly, Some Simple Exponent Rules
Before you check out the rest of this lens, keep 2 things in mind:
1) You cannot add numbers with exponents UNLESS they have the same exponent and base AND
2) The base (that is the number being raised to the power) needs to be the same to be able to multiply or divide them.
For example, you cannot add the terms in figure 1 because they have different exponents. You cannot simplify the terms in figure 2 because they have different bases (a, b and c).
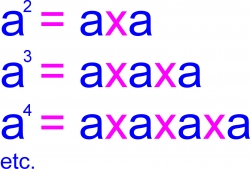
Explaining Exponents
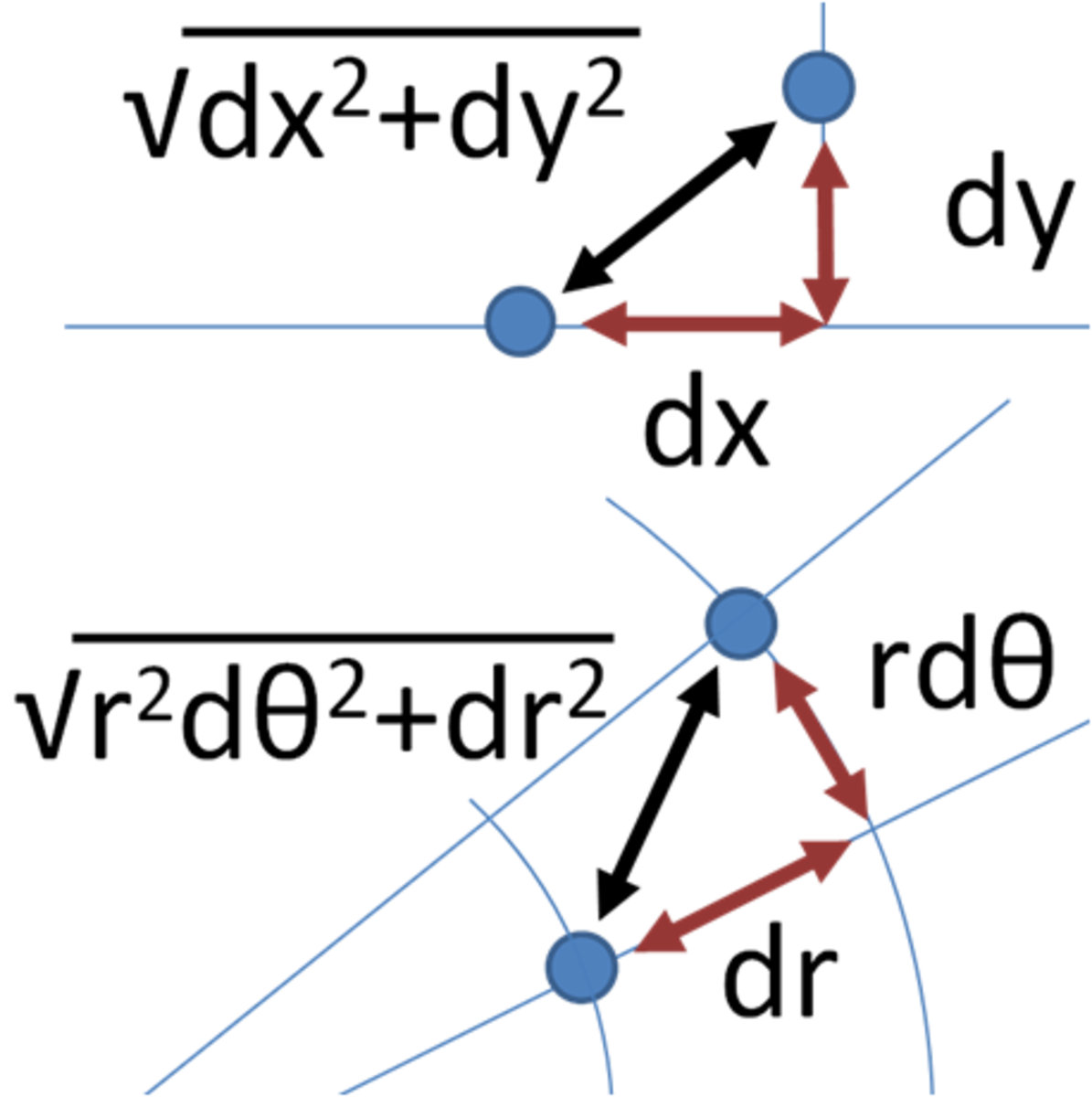
An exponent means that's how many times you multiply a number by itself. As you can see from the picture, A squared (that's A to the 2nd power) is A times A. A cubed (A to the 3rd power) is A times A times A. A to the 4th power is A times A times A times A.
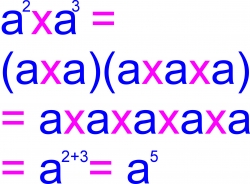
Multiplying Exponents
Multiplying numbers with exponents is relatively easy -- all you do is add the exponent.
If you look at the graphic, you can see why that works -- you are adding the "A"s in the multiplication problem. The "A" squared represents two "A"s multiplied by each other, the "A" cubed represents three "A"s multiplied by each other. So you add the "A"s and you get "A" to the fifth power.
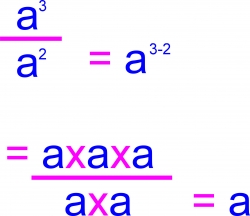
Dividing Exponents
Dividing exponents is pretty much just as easy as multiplying, but reversed. To divide numbers with exponents, you subtract the exponents. As you can see from this graphic, "A" cubed divided by "A" squared is "A" to the first, or "A".
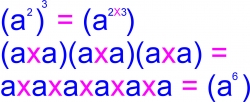
Raising an Exponent to Another Power
In order to raise an exponent to another power, you multiply the exponents. As you can see from the graphic, each "A" Squared appears three times -- so if you count the "A"s you will see there is a total of 6 "A"s.
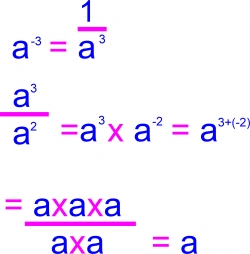
Negative Exponents
A negative exponent is just 1 over the same number exponent -- just as multiplying has you adding exponents, using negative exponents would have you add the exponents --
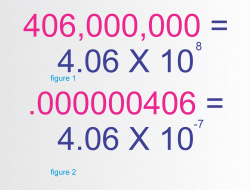
Scientific Notation
Scientific Notation is the term for using the powers of 10 (each of which represent one zero) to express complex numbers. For example, in the graphic as the right, 406,000,000 is difficult to deal with. So if you express this as 4.06 X 10 to the 8th power, then it is easier to work with. On the other hand, .000000406 is 4.06 X 10 to the -7 (that is 1/10 to the seventh power).
10 to the 8th power is a 1 with 8 zeroes, 100,000,000 and 4.06 times that means that the 4 would be where the 1 is in 100,000,000 and the .06 would follow the 4 into the next two spots in the number.
Learn more about Algebra from these books on Amazon

Math Themed Items from Compugraph Designs' Printfection Store
In addition to our Cafe Press and Zazzle sites (see modules above), we also have a store on "Printfection" which includes cutting boards (good wedding or housewarming gifts), mugs and cups, tees, etc.
This cutting board is only one of several Math themed items at our store:
(Click on the picture to go directly to this product's page)

Compugraph Designs Art Now Site
"Art Now" is another "Print on Demand" site. They have a nice collection of clocks and watches, including the one pictured here (with math symbols on it). Click on the picture to see the entire site.

Math Themed Items from Compugraph Designs' Printfection Store
In addition to our Cafe Press and Zazzle sites (see modules above), we also have a store on "Printfection" which includes cutting boards (good wedding or housewarming gifts), mugs and cups, tees, etc.
This mug is only one of several Math themed items at our store:
(Click on the picture to go directly to this product's page)