Classical Definition of Probability

Definition of Probability
Suppose an event (E) can happen in h ways out of a total of n possible equally likely ways. Then the probability of occurrence of the event (called a success) is denoted by:
p = P (E) = h/n
The probability of a non-occurrence of the event (called a failure) is denoted by
q = P (not E) = n-h/n = 1-p = 1- P (E)
Thus, p + q = 1 or P (E) + P (not E) = 1
So, the probability of an event is a number between 0 and 1. If the event cannot occur, its probability is 0. If an event is certain, its probability is 1. If p is the probability that an event will occur, the odds in favor of its happening are p: q (read this as “p to q”); the odds against its happening are q:p. The odds against a 3 or 4 showing up in a single toss of a fair die are q: p = 4/6: 2/6 or 4:2 which reduces to 2:1.

Single Event
-
The probability (P) of an event is equal to the number of possible outcomes corresponding to event (E) divided by the total number of outcomes. That is:
P (E) = # of event outcomes ¸ # of total outcomes
Example: The probability of drawing a spade from a deck of 52 cards is: 13/52 = .25.
Example: The probability of a coin toss resulting in heads is: 1/2 = .50.
Example: The probability of picking a red marble from a sack of 9 red, 6 blue, and 5 green marbles is: 9/20 = .45.
-
The probability of an event not occurring is 1 less the probability of the event occurring. That is:
P(not E) = [1 – P(E)]
Example: The probabilities for the three events above not occurring are .75, .50, and .55.
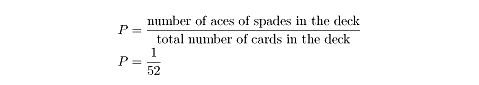
Multiple Independent Events
-
Two events are independent if the occurrence of one of the events gives us no information about whether the other event will occur; that is, the events have no influence on each other.
-
If two events, A and B, are independent, then the probability of BOTH events occurring at the SAME TIME is equal to the product of the probabilities of the two individual events. That is:
P(A and B) = P(A) x P(B).
Example: Suppose that a man and a woman each has a deck of 52 cards. Each draws a card from his or her individual deck. Find the probability that they BOTH draw the ace of clubs.
Define the events:
A = probability that the man draws the ace of clubs from his deck = 1/52
B = probability that the woman draws the ace of clubs from her deck = 1/52
Events A and B are independent so, P(A and B) = P(A) x P(B): 1/52 x 1/52 = 1/2704 = .00037
Therefore, the probability that both the man and woman draw the ace of clubs from their individual decks of cards is .00037. The probability of this event not occurring is (1 – P) = (1 - .00037) = .99963.
-
If two events, A and B, are independent, then the probability of BOTH events occurring ONE AFTER THE OTHER IN A SPECIFIED ORDER is the product of the probabilities of the two individual events. That is: P(A and B) = P(A) x P(B).
Example: What is the probability of the man drawing the ace of clubs and then the jack of hearts from his deck of cards (assuming the first card drawn is replaced in the deck before the second card is drawn; that is, he’s sampling with replacement)?
Define the events:
A = probability that the man draws the ace of clubs from his deck on the first draw = 1/52
B = probability that the man draws the jack of hearts from his deck on the second draw = 1/52
Events A and B are independent and order is important so, P(A and B) = P(A) x P(B): 1/52 x 1/52 = 1/2704 = .00037
Therefore, the probability that the man draws the ace of clubs and then the jack of hearts from his deck of cards is .00037. The probability of this event not occurring is (1 – P) = (1 - .00037) = .99963.
-
If two events, A and B, are independent, then the probability of BOTH events occurring ONE AFTER THE OTHER IN ANY ORDER is the sum of the probabilities of each event occurring separately. That is:
P(A or B) = P(A) + P(B).
Example: What is the probability of the woman drawing the ace of clubs and the jack of hearts from her deck of cards, regardless of order (assuming the first card drawn is replaced in the deck before the second card is drawn; that is, she’s sampling with replacement)?
Define the events:
A = probability that the woman draws the ace of clubs then the jack of hearts = 1/52 x 1/52 = 1/2704
B = probability that the woman draws the jack of hearts then the ace of clubs = 1/52 x 1/52 = 1/2704
Events A and B are independent and order is not important so, P(A or B) = P(A) + P(B): 1/2704 + 1/2704 = 2/2704 = .0007.
Therefore, the probability that the woman draws the ace of clubs and the jack of hearts from her deck of cards in any order is .0007. The probability of this event not occurring is (1 – P) = (1 - .0007) = .9993.
Multiple Mutually Exclusive Events
-
Two events are mutually exclusive if it is impossible for them to occur at the same time.
-
If two events, A and B, are mutually exclusive, then the probability of BOTH events occurring at the SAME TIME is equal to the product of the probabilities of the two individual events. This calculation will always result in 0. That is:
P(A and B) = P(A|B) x P(B|A) = 0 x 0 = 0.
Example: A coin is flipped one time. What is the probability of obtaining a heads (event A) and a tails (event B)?
Events A and B are mutually exclusive so they cannot occur simultaneously.
P(A and B) = P(heads given tails) x P(tails given heads) = 0 x 0 = 0.
Therefore the probability of obtaining a heads and a tails on one coin toss is zero.
-
Note: the probability formulas for independent and mutually exclusive events are the same but the terms ‘independent’ and ‘mutually exclusive’ are not synonymous. The probability for mutually exclusive events occurring at the SAME TIME will always be zero. This is not the case for independent events. See the previous section for independent events.

Multiple Non-Mutually Exclusive Events
-
Two events are non-mutually exclusive if they can occur at the same time. For example, a student can be both female and an engineering student at the same time.
-
The probability of either A or B occurring is the sum of the probability of A and the probability of B less the probability of A and B. That is:
P (A or B) = P(A) + P(B) - P(A and B). OR stated as: P (A or B) = P(A) + P(B) – [P(A) x P(B)].
Example: Find the probability of drawing either a king or a spade from a deck of 52 cards.
Define the events:
A = the probability of drawing a king = 4/52
B = the probability of drawing a spade = 13/52
Events A and B are non-mutually exclusive (one card is both a king and a spade) so,
P(A or B) = P(A) + P(B) - P(A and B): 4/52 + 13/52 – 1/52 = 16/52 = .3077
OR
P(A or B) = P(A) + P(B) - [P(A) x P(B)]: 4/52 + 13/52 – (4/52 x 13/52) = 832/2704 = .3077.
Therefore, the probability of drawing either a king or a spade from a deck of 52 cards is .3077. The probability of this event not occurring is (1 – P) = (1 - .3077) = .6923.







