Coordinate Line, Sets, and Intervals (Curious Concepts Precalculus 1.5)

Self-explain Learning Technique help people to better comprehend and remember any thing they want to learn. It my sound strange, but it is many times more effective then re-reading. To use this technque, give short answers to the prompted questions. The more privious knowlege that you incorperate into your answer, the more effective this learning technique is. On average it improves learning by over 2.5 standard deviations; the difference between a C student and an A student.

How could a solid understanding of math's basic structure help you?

The Coordinate Line has an Origin at the point of 0 (kinda coincidental huh). All real numbers can be plotted on it. From this Origin at 0: Natural Numbers ascend to the right, negative Integers descend to the left, Rational and Irrational numbers are plotted at their true-or-approximate values.

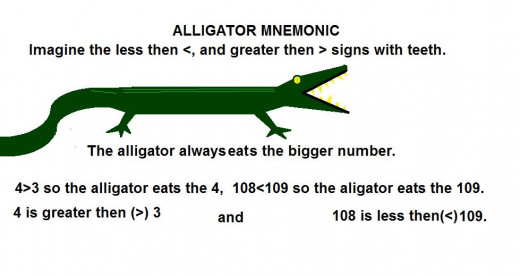
There is an inherent order to the coordinate line that can be expressed by relationships. We can say that a is greater then b by writing a>b if a-b>0; that is a minus b is greater then 0. We can say that a is less then b by writing a<b if a-b<0. You should be, or soon get, very familiar with this notation; but I still use the alligator always eating the bigger number mnemonic when things get complicated. The greater then sign can be modified to create ≥, meaning equal to or greater then. The less then sign can be modified to create ≤, meaning equal to or less then.

If you had a pocket full of change; you could concider each denomination an set, and the year the coin was made an element. How could you apply sets and elements to more then chump change?

Sets

A collection of objects (numbers) is called a Set, and each object (number)is call an Element. The element symbol, ε, is used to express this relationship. a ε B is read as a is an element of B.

What would you expect the meaning of the element symbol with a line through it would mean? It means "not an element", as in meaning c is not an element of D.

Sets can be made by listing elements inside of braces.

Example: K={2,3,4,5,6}

We can also use K in a set-builder notation. correspondingly

Example: K={x│x is an integer and 1<x<7}

This is read: K is the set of all x; such thatx is an integer and 1 is less thanx, and x is less then 7.

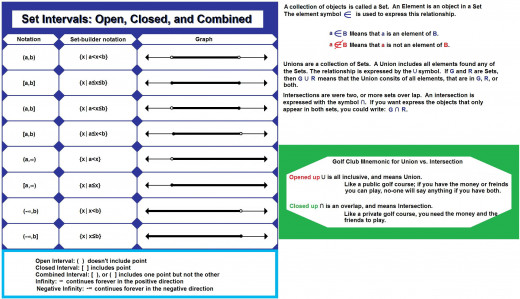
Unions are a collection of all elements in more then 1 set, and the relationship is expressed by the symbol. If G and R are Sets, then there Union includes all elements that are in G, and R, or both.

A Union of pionts that appear in both Sets, G and R is writen as: G U R

Intersections are were two or more sets over lap, and are expressed with the symbol ∩. If L and M are Sets, then there intersection includes only elements that are found in both L and M.

If you want express the objects that only appear in both sets L and M , you could write: L ∩ M

Unions include all the objects in both sets. An object only needs to fall into one of the sets being combined to be included. Intersections are were the sets overlap, an object needs to be part of both sets.

How would you compare rocks and hard places to intervals?

Intervals are sets of real numbers and are very common in calculus. Intervals correspond to line segments.

The Open Interval between two points, points a and b,are shown as open circles at their points on a graph. a < b, is denoted with parentheses (a,b), and consists of all possible points between a and b, but not a and b.

The Closed Interval includes the end points a and b , a ≤ b, along with all the points between them; a ≤ b. Closed intervals are denoted with brackets: [a,b]. The points a and b are shown as filled circles at their points on a graph.

Using set-builder notation, we write:

(a,b) = {x│a<x<b} [a,b] = {x│a≤x≤b}

They are shown as on a line graph:

(a,b)

<---------------------o================o------------------------->

[a,b]

<--------------------------●==================●---------------->

The Combined Interval uses both, parentheses and brackets, to show that one end point is included but the other is not.

If only one end point exists, the infinity symbols, ∞ or -∞, can be used to show that a set continues to infinitely in one direction.