Floyd's algorithm source code in C
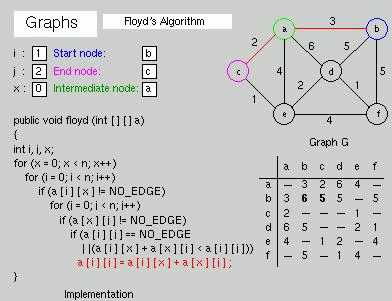
Algorithm
The Floyd–Warshall algorithm compares all possible paths through the graph between each pair of vertices. It is able to do this with only Θ(|V|3) comparisons in a graph. This is remarkable considering that there may be up to Ω(|V|2) edges in the graph, and every combination of edges is tested. It does so by incrementally improving an estimate on the shortest path between two vertices, until the estimate is optimal.
Consider a graph G with vertices V, each numbered 1 through N. Further consider a function shortestPath(i, j, k) that returns the shortest possible path from i to j using vertices only from the set {1,2,...,k} as intermediate points along the way. Now, given this function, our goal is to find the shortest path from each i to each j using only vertices 1 to k + 1.
There are two candidates for each of these paths: either the true shortest path only uses vertices in the set {1, ..., k}; or there exists some path that goes from i to k + 1, then from k + 1 to j that is better. We know that the best path from i to j that only uses vertices 1 through k is defined by shortestPath(i, j, k), and it is clear that if there were a better path from i to k + 1 to j, then the length of this path would be the concatenation of the shortest path from i to k + 1 (using vertices in {1, ..., k}) and the shortest path from k + 1 to j(also using vertices in {1, ..., k}).
If w(i,j) is the weight of the edge between vertices i and j, we can define shortestPath(i, j, k) in terms of the following recursive formula: the base case is
shortestPath(i,j,0) = w(i,j)and the recursive case is
This formula is the heart of the Floyd–Warshall algorithm. The algorithm works by first computing shortestPath(i, j, k) for all (i, j) pairs for k = 1, then k = 2, etc. This process continues until k = n, and we have found the shortest path for all (i, j) pairs using any intermediate vertices.
Floyd's Algorithm
/*C PROGRAM TO IMPLEMENT ALL PAIR SHORTEST PATH USING FLOYDS ALGORITHM
INPUT: N VALUE FOR NUMBER OF VERTICES
OUTPUT: ADJACENCY MATRIX
SHORTEST DISTANCE MATRIX
*/
#include<stdio.h>
#include<stdlib.h>
void AdjacencyMatrix(int a[][100],int n){ //To generate adjacency matrix for given nodes
int i,j;
for(i = 0;i < n; i++)
{
for(j = 0;j <= n; j++)
{
a[i][j] = 0;
}
}
for(i = 1; i < n; i++)
{
for(j=0;j<i;j++)
{
a[i][j] = rand()%10;
a[j][i] = 99;
}
}
}
int min(int a,int b){
if(a < b)
return a;
else
return b;
}
void floyds(int a[][100],int n){
int i,j,k;
for(k = 0;k < n ; k++)
{
for(i = 0;i < n; i++)
{
for(j = 0;j < n ; j++)
{
a[i][j] = min (a[i][j], a[i][k] + a[k][j] );
}
}
}
}
int main()
{
int a[100][100],n,i,j;
FILE *fp = fopen("floyds.dot","w"); /* FOR DIGRAPH */
fprintf(fp,"digraph A {\n"); /* WRITE TO FILE */
printf("Enter the vertices of the digraph\n");
scanf("%d",&n);
AdjacencyMatrix(a,n);
printf("\t\tAdjacency Matrix of the graph\n"); /* PRINT ADJACENCY MATRIX */
for(i = 0;i < n; i++)
{
for(j = 0;j < n; j++)
{
printf("\t%d",a[i][j]);
if(a[i][j] != 0)
{
fprintf(fp,"%d -> %d\n",i,j);
}
}
printf("\n");
}
floyds(a,n);
printf("\n Shortest distance matrix\n"); /*PRINT SHORTEST DISTANCE MATRIX*/
for(i = 0;i < n; i++)
{
for(j = 0;j < n; j++)
{
printf("\t%d",a[i][j]);
}
printf("\n");
}
fprintf(fp,"}\n\n");
fclose(fp);
return 0;
}