What is the radius of circle if the pink area equals the green one?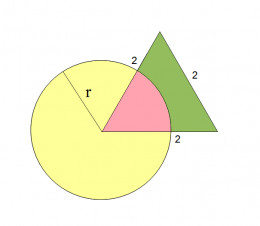
Because the triangle is equilateral, the angle for the pink area is 60 degrees, which is 1/6 of the 360 degree circle. So the area of the pink shaded region is pi * r^2 / 6.
The height of the triangle is sqrt (4 - 1) = sqrt (3). Which makes the area of the whole triangle= sqrt (3) * 2 / 2 = sqrt (3). So the area of the green shaded region = area of the whole triangle - area of the pink shaded region = sqrt (3) - pi * r^2 / 6.
Given that the area of the pink shaded region = area of the green region, we get the following equation:
pi * r^2 / 6 = sqrt (3) - pi * r^2 / 6
Solving for r:
pi * r^2 / 3 = sqrt (3)
r^2 = 3 * sqrt (3) / pi
r = sqrt [3 * sqrt (3) / pi]
Since the area of the triangle is sq rt 3, then pi r^2/6 must equal (rad 3)/2. cross multiplying and dividing by 3 and simplifying gives approximately 1.654 = r^2 taking the sq rt of each side gives approximately 1.286.
Both solutions are correct! (so I select the first answer as the best) The area of triangle is sqrt(3), and than we use formula for the pink area: A=r^2 *pi * alpha /360, where the angle alpha is 60 (since we have equilateral triangle).
by flysky 12 years ago
What is the area of pink triangle?
by Suann1993 11 years ago
how does the ionic radius of a typical metal compare with a atomic radius?
Copyright © 2025 The Arena Media Brands, LLC and respective content providers on this website. HubPages® is a registered trademark of The Arena Platform, Inc. Other product and company names shown may be trademarks of their respective owners. The Arena Media Brands, LLC and respective content providers to this website may receive compensation for some links to products and services on this website.
Copyright © 2025 Maven Media Brands, LLC and respective owners.
As a user in the EEA, your approval is needed on a few things. To provide a better website experience, hubpages.com uses cookies (and other similar technologies) and may collect, process, and share personal data. Please choose which areas of our service you consent to our doing so.
For more information on managing or withdrawing consents and how we handle data, visit our Privacy Policy at: https://corp.maven.io/privacy-policy
Show Details| Necessary | |
|---|---|
| HubPages Device ID | This is used to identify particular browsers or devices when the access the service, and is used for security reasons. |
| Login | This is necessary to sign in to the HubPages Service. |
| Google Recaptcha | This is used to prevent bots and spam. (Privacy Policy) |
| Akismet | This is used to detect comment spam. (Privacy Policy) |
| HubPages Google Analytics | This is used to provide data on traffic to our website, all personally identifyable data is anonymized. (Privacy Policy) |
| HubPages Traffic Pixel | This is used to collect data on traffic to articles and other pages on our site. Unless you are signed in to a HubPages account, all personally identifiable information is anonymized. |
| Amazon Web Services | This is a cloud services platform that we used to host our service. (Privacy Policy) |
| Cloudflare | This is a cloud CDN service that we use to efficiently deliver files required for our service to operate such as javascript, cascading style sheets, images, and videos. (Privacy Policy) |
| Google Hosted Libraries | Javascript software libraries such as jQuery are loaded at endpoints on the googleapis.com or gstatic.com domains, for performance and efficiency reasons. (Privacy Policy) |
| Features | |
|---|---|
| Google Custom Search | This is feature allows you to search the site. (Privacy Policy) |
| Google Maps | Some articles have Google Maps embedded in them. (Privacy Policy) |
| Google Charts | This is used to display charts and graphs on articles and the author center. (Privacy Policy) |
| Google AdSense Host API | This service allows you to sign up for or associate a Google AdSense account with HubPages, so that you can earn money from ads on your articles. No data is shared unless you engage with this feature. (Privacy Policy) |
| Google YouTube | Some articles have YouTube videos embedded in them. (Privacy Policy) |
| Vimeo | Some articles have Vimeo videos embedded in them. (Privacy Policy) |
| Paypal | This is used for a registered author who enrolls in the HubPages Earnings program and requests to be paid via PayPal. No data is shared with Paypal unless you engage with this feature. (Privacy Policy) |
| Facebook Login | You can use this to streamline signing up for, or signing in to your Hubpages account. No data is shared with Facebook unless you engage with this feature. (Privacy Policy) |
| Maven | This supports the Maven widget and search functionality. (Privacy Policy) |
| Marketing | |
|---|---|
| Google AdSense | This is an ad network. (Privacy Policy) |
| Google DoubleClick | Google provides ad serving technology and runs an ad network. (Privacy Policy) |
| Index Exchange | This is an ad network. (Privacy Policy) |
| Sovrn | This is an ad network. (Privacy Policy) |
| Facebook Ads | This is an ad network. (Privacy Policy) |
| Amazon Unified Ad Marketplace | This is an ad network. (Privacy Policy) |
| AppNexus | This is an ad network. (Privacy Policy) |
| Openx | This is an ad network. (Privacy Policy) |
| Rubicon Project | This is an ad network. (Privacy Policy) |
| TripleLift | This is an ad network. (Privacy Policy) |
| Say Media | We partner with Say Media to deliver ad campaigns on our sites. (Privacy Policy) |
| Remarketing Pixels | We may use remarketing pixels from advertising networks such as Google AdWords, Bing Ads, and Facebook in order to advertise the HubPages Service to people that have visited our sites. |
| Conversion Tracking Pixels | We may use conversion tracking pixels from advertising networks such as Google AdWords, Bing Ads, and Facebook in order to identify when an advertisement has successfully resulted in the desired action, such as signing up for the HubPages Service or publishing an article on the HubPages Service. |
| Statistics | |
|---|---|
| Author Google Analytics | This is used to provide traffic data and reports to the authors of articles on the HubPages Service. (Privacy Policy) |
| Comscore | ComScore is a media measurement and analytics company providing marketing data and analytics to enterprises, media and advertising agencies, and publishers. Non-consent will result in ComScore only processing obfuscated personal data. (Privacy Policy) |
| Amazon Tracking Pixel | Some articles display amazon products as part of the Amazon Affiliate program, this pixel provides traffic statistics for those products (Privacy Policy) |
| Clicksco | This is a data management platform studying reader behavior (Privacy Policy) |


