Math Hints: Algebra -- Difference of Squares

Factoring Trick
Algebra students often have to factor polynomials on their exams. Since tests are generally timed, most students would welcome anything that would save them time.
One thing that can make a test quicker is "Difference of Squares". If you can master this concept, you can save yourself a lot of time on standardized math test.
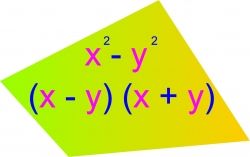
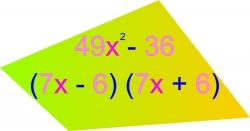
The Difference of Squares: What does it mean?
The Difference of Squares is an interesting mathematical anomaly. In most cases, when you take two binomials (that is an equation of two different bases, as in one being a constant and the other being a variable and adding them together -- for example (2x+7) or (x-5) or even (3x+4y)) that have the same bases (for example (2x+7) times (4x-5) or (y-5) times (y+3) or even (2x+y) times (x-3y)) you end up with a trinomial (that is a three base answer -- for example (8x [squared] +18x-35) or (y [squared] -2y-15) or 2x [squared] -5xy-3y [squared]) respectively.
The picture here shows this concept in its most basic form (x and y can each be any number, variable or combination of number and variable that is a perfect square, like 4, 9, 16, x [squared], 16x [to the 4th power], etc.)
An Example:
In the picture here, since 49 and 36 are perfect squares (49 being 7 [squared] and 36 being 6 [squared]), this works with this equation pictured here.

Why does it work this way?
Notice what happens if you multiply (7x-6) and (7x+6) -- from right to left -- (+6) times (-6) equals (-36), (+6) times (7x) equals (+42x), (-6) times (7x) equals (-42x), (7x) times (7x) equals (49x [squared]) {see the middle section on the picture}.
If you notice, the middle products ( (+42x) and (-42x) ) will cancel each other out {see the line through them} because (+42x) + (-42x) = 0.
The ultimate product {see the bottom line in the picture} ends up being (7x) [squared] {which is 49x [squared]} minus 6 [squared] {which is 36}.
So, you can apply this to factoring -- if you see a set up that is (x+y) times (x-y) you know the answer will be (x [squared] - y [squared]) (see the picture above). And, if you see a set up of (x [squared] - y [squared]), then you know it factors out to (x+y) times (x-y).
Note: this will NOT work with (x [squared] + y [squared]) -- it only works with (x [squared] - y [squared]) -- this is it only works with a difference of squares, not a sum of squares.

Compugraph Designs' Spoonflower Shop
Buy your fabrics on Spoonflower
If you sew, Spoonflower is a great place to find unusual fabric patterns and designs.