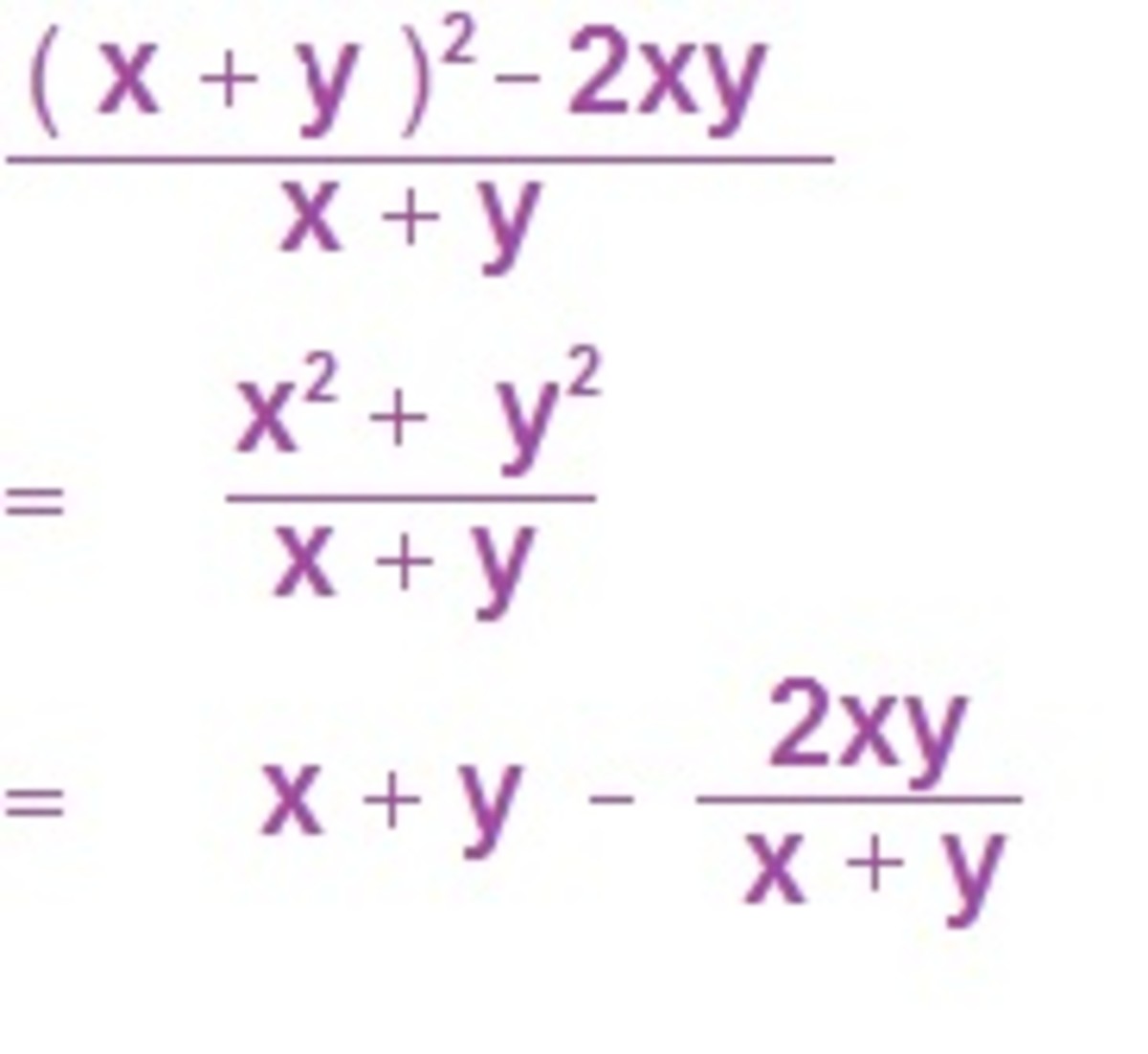Whats with the math mysteries?

Dear math teacher, I’m writing this letter to inform you that I would have wanted to continue with your lessons but I’m disappointed by your inefficacy to answer my questions.

First of all, before we embark on anything you always told me that I should base everything on numbers. The problem is up-to now I have never known where I should start counting from. I’m sure there is a range but you always talk of epsilon as being the smallest known number and infinity as being the largest. Now this is confusing since the Greeks for some reason think epsilon is a letter and not a number. On the other end of the tunnel, there is always infinity which all of you claim to know but none have ever reached there.

Between 0 and 1, I was introduced to a myriad multiple of difficult numbers which you decided to call fractions. However, I came to realize soon that these were not numbers but incomplete divisions. I’m yet to understand why anyone else has never bothered to do these divisions so that we can end up with proper decimals.

Then I stumbled upon letter j in mathematics but in this case I’m told it’s supposed to have a meaning. Somebody somewhere decided that a negative number should have a square root. The only thing that I blamed them for is that they always invent answers which are nothing short of this j! We knew the square root of 49 to be 7, 4 to be 2 and it was good. But this guy came with a metaphorical j that was attached to the roots of -49, -4 and whatever else that could be negative!!! Cool. I do not hate on the j idea. Only that it doesn’t help because j is just too complex to exist in the first place. Could we possibly drop this fantasy of j and decide that a negative number would never need a square root?

One of the famous ways to do multiplication was by manipulating logarithms and fetching an antilogarithm. It was easy until I began to understand just what a logarithm was. I’m told the logarithm of 100 to base 10 is 2 because two 10’s are enough to be multiplied together to get 100. That was fine. But wait till I shifted the base to one. I sat the whole day long and figured just how many ones I needed to multiply together to get 100… Perhaps I should have added the 1s. Life would then be easier. But then that would never be a solution, so I left it as 1 to power N. Don’t worry, I would be disclosing the N soon.

And then there is one more thing, it’s ‘probably’ the one in ten. Nobody’s knows it. If you have done statistics, you ‘probably’ know what I’m talking about. I think one in ten people must have read this document. No matter how long I do these numerous approximations, I would never point you out.
Yet from a statistics point of view I’m supposed to be sure that you did, heck I can’t be!