mental Calendar

We all need a calendar, we have to depend on the printed calendar to find the weekday of a particular date, which is sometimes unavailable. So it would be great if we can calculate it mentally. We can use the Zeller's congruence if we have a calculator in our hand, otherwise I found the Doomsday rule to calculate the week day of a particular date very convenient and it is so easy that we can calculate it mentally very quickly. I shall discuss the doomsday rule to find the weekday of any calendar date mentally in this hub

This algorithm takes advantage of the fact that each year has a certain weekday (the doomsday) upon which certain easy-to-remember dates fall. The algorithm is simple enough for anyone with basic arithmetic ability to perform the calculations mentally.
First, we need to remember certain days of a month, the memorable dates in the calendar year are :

the last day of February (28th or 29th day whichever is applicable considering the leap year)
4th day of April or the 4th Month;
6th day of June or the 6th Month;
8th day of August or the 8th Month;
10th day of October or the 10th Month;
12th day of December or the 12th Month;
Remembering the above dates for even months is pretty easy, the odd months we need to remember (5, 9) and (7, 11), that is:
5th day of September or the 9th Month;
9th day of May or the 5th Month;
7th day of November or the 11th Month;
11th day of July or the 7th Month;
Remains the 3rd month which is the 7th day of March;
and for January is the 3rd day in normal years or the 4th day in leap years.

• I have arranged the 12 months of the year in groups such that it can be memorized easily. Leap year calculation is required for January and February months only.

As said, all the above easy-to-remember dates fall in the same weekday in every calendar year. for example in the year 2012 all the above memorable dates was Wednesday, in the year 2013 is Thursday, in the year 2014 is Friday and in the year 2015 is Saturday.

Now, the method is to choose the closest date that always fall on the doomsday and count the number of days (MOD 7) between that date and the date in question to compute at the day of the week. We can however further extend this calculation beyond centuries, for simplicity I'll discuss that later.

Illustrating with an example

I wish to find the weekday of 25-Dec-2012, I knew that 12th December 2012 (the doomsday) was Wednesday, so is (doomsday±7n; n=1,2,3,4,..) 26th of December, thus Christmas Day in 2012 was a day before Wednesday, which is Tuesday. Fortunately, Christmas Day is always the day before the Doomsday.

So, if we can calculate the difference of days with the doomsday and perform a simple division by 7, we can easily find the weekday for any date of the calendar year. Practice the same keeping a printed calendar, to test your progress and hope to become fluent in no time.

The Doomsday algorithm for mental calculation was devised by John Conway to quickly calculate the weekday of any given date without the help of calculators or calendars. Conway's algorithm bases on the fact that some certain easy to remember dates always fall on the same weekday within any given year. We know that these dates are called doomsdays.

Now, its time to find the doomsday of a year in question, so that we are not just limited in calculating for the current year only.

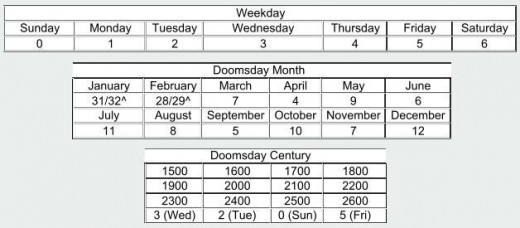
Each weekday is represented by a number.
Sunday → 0; Monday → 1; Tuesday → 2; Wednesday → 3; Thursday → 4; Friday → 5; Saturday → 6.

Next, we have to remember the anchor day for centuries, as the Gregorian calendar cycles every 400 years, it is sufficient to remember the anchor days for 4 centuries.
18xx → 5; 19xx → 3; 20xx → 2; 21xx → 0.

The steps for finding the doomsday of any given year. [yy is the last two dizits of the year in question].
1. Let P = yy \ 12; //taking the floor of the quotient
divide the last two dizits of the year by 12 and take the result discarding the remainder.
2. Let Q = yy MOD 12; // modulo operation.
divide the last two dizits of the year by 12 and take the remainder part.
3. Let R = Q \ 4; // floor(q ÷ 4).
divide the result obtained in Step 2 by 4, discarding the remainder.
4. weekday of the century anchor day (W), eg. 19xx→3.
20xx → 2; 21xx → 0; 22xx → 5; and the cycle continues (anchor day for centuries)
5. Let S = P + Q + R + W; // sum up of above 4 steps.
6. doomsday of the year = S MOD 7 = weekday represented by the number.

taking an example, we wish to find the doomsday of the year 2013
Here, Century cc=20xx and Year yy=13.
1. P = 13 divided by 12 discarding the remainder is 1
2. Q = 13 divided by 12 considering the remainder is 1
3. R = 1 divided by 4 discarding the remainder, quotient is 0
4. W = 20xx → 2 (anchor day for centuries, given in the chart)
5. S = 1+1+0+2 = 4
6. doomsday of the year 2013 = 4 % 7 = 4 is Thursday (weekday is represented by the number).

After finding the doomsday of the year, we choose the closest date that always fall on the doomsday (±7n) and count the number of days (MOD 7) between that date and the date in question to find the day of the week.

I shall also discuss another method here to find the weekday of a month of any year between 1900 to 2099. I personally feel this range is sufficient when considering the mental calculations, you may however like to extend this further by altering the century code given, that is also pretty simple.

The formula :

Let dd/mm/yy be the date in question for which we need to compute the week day.

1. Month-Code for the twelve months is 033 614 625 035 (January to December respectively);
2. Century=6; // 20xx→6 and 19xx→0, I'm taking 6 for the present century.
3. leapCode:=floor(yy÷4); // integer part of the quotient.
4. If (LEAP_YEAR AND (MONTH is Jan OR MONTH is Feb)) then leapCode:=leapCode-1;
5. DAY:=(Century + dd + Month-Code + yy + leapCode) MOD 7;
6. The Day computed in step 5 is in range 0-6 which is from Sunday to Saturday respectively.

Examples

Example 1: Date 14 08 1947
Century = 0, 19xx=0
Month Code = 2, August=2
Leap Code = 11, floor of quotient when 47 divided by 4
Day = (0 + 14 + 2 + 47 + 11) MOD 7 = 4 which is Thursday.

Example 2: Date 01 01 2015
Century = 6, 20xx=6
Month Code = 0, January=0
Leap Code = 3, floor of quotient when 15 divided by 4
Day = (6 + 1 + 0 + 15 + 3) MOD 7 = 4 which is Thursday.