The Millennium Prize Problems: Incentivizing Modern Mathematics

Fermat’s Last Theorem departed the list in 1994, when UK Mathematician Andrew Wiles submitted his successful proof of the theorem. He worked on it tirelessly throughout his career and finally submitted a proof that was flawed. After going back to the drawing board, he happened upon a moment of insight, at which point he was able to integrate early methods with modern mathematical discoveries to come up with an accepted proof.

In 2003, the Poincare Conjecture, another of the Millennium Prize's original problems, was successfully proven by Grigoriy Perelman. The proof was recognized by the Clay Institute in 2010 after scrupulous error checking and minor polishing, but Perelman refused the $1 million Millennium Prize.
Who Wants to Be a Millionaire
What would you do with one million dollars? The millennium has plowed fields ripe for financial harvest -- these days, millionaire is commonplace vocabulary. With many of the world’s financial elite making a buck (and by buck, read: more than a million dollars) from smart investing, well-timed startup and app rollouts, real estate, and steadfast corporate drive, our society paints a picture of success that is akin to survival of the fittest. For the rest of us: what would you do with one million dollars?
Are you good at math? Are you very good at math? Are you willing to devote the rest of your career to providing a reasonable proof for a thus unproved theorem or conjecture? The Clay Mathematics Institute offers the Millennium Prize -- $1 million and worldwide recognition -- to any person capable of such a feat.
*Disclaimer: this is a math-heavy hub.


P = NP?
P versus NP
The relationship of P and NP is neither easy to define nor to conceptualize. In the problem -- classically posed as P = NP? (Does P equal NP?) -- mathematicians, computer scientists, and physicists explore the time required for an algorithm to find a solution compared to the time required for an algorithm to check the validity of a solution. To elaborate, P represents the problems whose solutions are solved in polynomial time with respect to the number of elements handled by the algorithm. That is, there exist some problems who have “N” elements, and the solutions solved in a timeframe proportional to a polynomial of “N” (i.e. N^3 + N^2) are part of the set P. The problems whose verification time have similar polynomial proportionality are part of the set NP. The question thus asks us: if a solution can be determined in polynomial time (as part of the set P), can it also be verified in polynomial time (as part of the set NP), and vice versa.
Computer scientist and mathematician Stephen Cook introduced the problem in 1971, in a paper entitled "The Complexity of Theorem Proving Procedures." Cook personally conjectures that there are problems in which P likely does not equal NP, and postulates that proof or disproof of the problem could revolutionize algorithm design, but also create a new tool in philosophical analyses.
Further information can be found on MIT’s review of the problem along with its practical applications.

Is it worth $1 million?
The Birch and Swinnerton-Dyer Conjecture
One of the most abstract and difficult math problems presented on this list, the Birch and Swinnerton-Dyer Conjecture presents a possible outcome of solutions in Number Theory. The basis of the conjecture begins in a much more complicated analysis of solution spaces for an elliptical curve. Without plunging into the ice, imagine that an elliptical curve is defined by all of the points the make p that curve -- which is reasonably true. Now consider the existence of an L-function, which essentially analyzes the behavior of the “points” of the ellipse continuously and beyond our scope for an infinite space.
The behavior of the solutions was analyzed for an ellipse having infinite solutions by Birch and Swinnerton-Dyer. They noticed an anomaly and stated it as a conjecture. Their conjecture essentially states that this L-function must have a zero value at a fixed point, or several related points. Though the conjecture was so stated by Birch and Swinnerton-Dyer following exploration of the issue using computer analysis for enormous data, the mathematics of the problem are attributed to number theory pioneer L. Mordell.
In reality, the conjecture is much more complicated and requires advanced understanding of number theory and topology concepts which may be inappropriate to provide in a hub. The Clay Mathematics Institute has kindly provided this write up of the conjecture by Andrew Wiles (of Fermat’s Last Theorem).

Have an hour to kill?

Yang-Mills Theory Existence and Positive Mass Gap
Yang Mills is probably the most physics-based problem listed. The problem states questions the existence and behavior of gauge groups, the effective Yang-Mills theory in real 4-space (the fourth dimension of real numbers), and whether this can predict a mass gap. Here is the exact problem: “Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on R4 and has a mass gap ∆>0. Existence includes establishing axiomatic properties at least as strong as those cited in [45, 35].” A gauge group is a certain symmetry group that exists around the space of an invariant function of a dynamic system called a Lagrangian. To make matters worse, gauge theory is not completely understood as it is, and an example of it does not yet exist in 4-space. Basically, the tools are not yet there to even tackle this theory.
What the Quantum Yang-Mills theory proposes is this: if there is a mass gap that is greater than zero, meaning that the smallest particle has mass, then an occurrence called clustering will occur -- this all occurring analytically, of course. When such an occurrence is witnessed, mathematicians claim it will provide them with a solution for the translation from real 4-space to any 4-space manifold, which has endless uses in the expanding field of topology.
This is, again, a problem best explained by the folks at Clay, who present this formal consideration of the Quantum Yang-Mills theory, by the esteemed and notable Edward Witten and Arthur Jaffe.

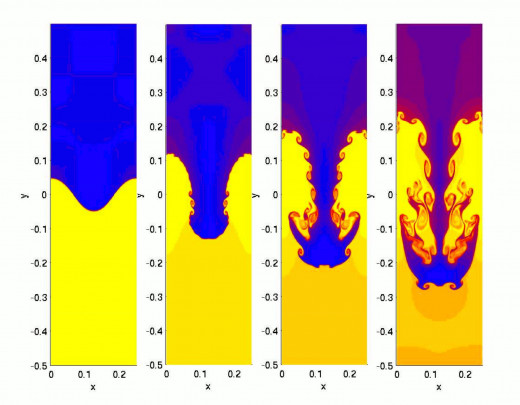
Navier–Stokes Existence and Smoothness
Critical to physical systems, fluid mechanics, and engineering design, the Navier-Stokes equations describe the motion of fluids in 3-dimensional space. The problem encountered with solving the equations is that they are non-linear differential equations that are dependent on differential entropy of any point in the system. Additionally, the equations are elliptical in nature. And although this problem can’t be solved, the equations are far from useless. Many specific solutions have been found that satisfy the equations; however, a general solution is yet to be discovered.
The Clay Institute poses this problem: “In three space dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, which are both smooth and globally defined, that solve the Navier–Stokes equations.” Thus, the general solution found should be represented by a solution field which is smooth, or continuous and differentiable, and globally defined. The main roadblock for pursuits of the solution is that turbulence is accounted for in most known solutions, yet its entropic nature forgoes reason and interpolation.
Aside from the prize, solving the Navier-Stokes equations would result in ultra-efficient aerodynamic design, super-liquids with ideal properties, a greater understanding of fluid motion, and a slew of other beneficial applications. Read the Clay Institute’s presentation of the problem in an overview by Charles Fefferman.


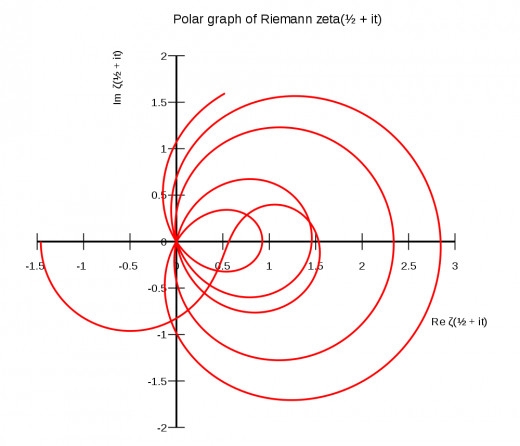

The Riemann Hypothesis
The Riemann Hypothesis is an exploration of prime numbers at heart. Famed mathematician G. F. B. Riemann did lots of work concerning prime numbers in pursuit of a pattern. His reasoning was that if so many prime numbers naturally occurred, then surely they occurred in some sort of order, or perhaps their order is certainly governed by some function. After much research, Riemann noticed that prime numbers did, in fact, relate in frequency to a zeta function -- ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ... – which has come to be aptly named the Riemann zeta function. Riemann hypothesized that the interesting solutions to ζ(s) = 0 lie on a vertical line. Officially, “the non-trivial zeros of ζ(s) have real part equal to ½,” the ½ representing the vertical line. In a nutshell, there is a pattern to the chaos, and the prime numbers follow a define curve stochastically.
Many mathematicians consider this revelation, if proven, one of the most important discoveries in pioneering pure mathematics and prime number theory. On the contrary, it would not sit well knowing that prime numbers, which are all related by nature, exist in no particular order or pattern. Thus far, the first 10,000,000,000 (10 billion) solutions have satisfied the Riemann hypothesis, but a generalization still cannot be made about its validity. The Clay institute provides both a generalized problem discussion with progress notes, and a deeper analysis of the hypothesis.



The Hodge Conjecture
Imagine that you need to drive a nail into a board. You pick up your hammer and you drive it in; simple, no? You continue to drive other nails in and realize the importance of this tool to your progress. However, you look down and realize that the tool is not exactly hammer -- rather, it approximates a hammer. You know that it works like a hammer, and looks hammer-esque, but you also know that it is not a hammer -- so what is it?
Such is the case in the Hodge Conjecture. Mathematicians began work on manifolds in two distinct schools of thought: the algebraic approach and topological exploration of a manifold. At some point, both approaches met the same challenge of arbitrary geometric or algebraic classes on a manifold. Enter William Hodge, who was able to develop and discover relationships between differential geometry and algebraic geometry, which connected the two worlds. The only problem was that he was using tools that were not verified -- imaginary tools, if you will. Hodge was meddling in the universe complex manifolds with great poise, and making steady progress doing so. It was at this point that Hodge conjectured “On a projective non-singular algebraic variety over [C], any Hodge class is a rational linear combination of classes cl(Z) of algebraic cycles.” Or, in English: “Let X be a non-singular complex projective manifold. Then every Hodge class on X is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X.” Basically, that the classes that make up X are a linear combination of the sub-manifolds of X. The intention of this conjecture was to simply clarify the tool he was using and add the complex subvarieties of manifolds to the generalized definition of de Rham Cohomology.
The problem did not initially receive that much attention, but Hodge convinced the Clay Institute why it was critical to both algebraic and geometric topology, and why the world’s great minds should take a second glance. A short write-up of the conjecture is found on the Clay Institute’s website, though it is mostly a perspective on possible routes to discover a proof and its possible outcomes.

Here is a nice summary of the Millennium Prize problems from the Clay Institute's millennium conference.
*The mathematics involved in this hub are still under investigation, not to mention extremely conceptual, intangible, and abstract. If you need clarification of some of the concepts discuss, please leave a comment and I will do my best to answer.
© 2014 sehrm