Neural Networks: A Beginner's Understanding
Consider the human brain. It consists of billions of interconnected neurons with each neuron being able to transfer information to many other neurons in the brain.
A neuron can be in
either a state of firing or in a state of rest. A neuron is fired, or
activated, when it receives and combines signals from many other
neurons and then produces an output which it sends to other neurons. A
neuron inputs the signals through connecting structures called
dendrites. The neuron combines the signals and produces a signal which
is output along a path called an axon. Synapses are the pathways
between the axons and dendrites through which the information must pass.
Neurons fire at different rates and the function of their physical
states is to convey information to other neurons. This simple transfer
of information is chemical in nature and the amount of signal
transferred depends on the amount of chemicals released in the brain
region at the time. When the brain learns, the efficiency of the
chemical transfer of information from the output of one neuron to the
inputs of many neurons is modified.
This transfer process
between neurons occurs in parallel which enables the brain to carry out
its many functions and to do many of them at the same time. For
example, the brain can take in sensory information, interpret this
input and send out signals to the muscles to produce a movement while
at the same time as seeing, hearing and carrying out a conversation.
Thus,
the brain can be thought of as an information-processing system which
can do many things at the same time. An attempt to understand how the
brain functions has been made by emphasising the computational ability
of the brain and creating simplified models of how neurons in the brain
function. By modeling how the brain works through computation it is
possible to explain some of the brains' functions, such as perception,
imagery and motor action, in ways which mirror the brain's ability to
carry out these functions.
THE CONCEPT OF CONNECTIONISM
What is Connectionism?
Connectionism (or parallel distributed processing) describes the use of computational models which consist of neuron-like units which work together to process information interactively and in parallel. These computational models (neural networks) aim to model the way the human brain processes information and hence to model human behaviour. Neural networks operate by mapping various inputs on to particular outputs and by storing these associations between inputs and outputs in the networks
The Components of a Connectionist Architecture
The
brain is considered to be a network, consisting of simple units which
are connected to each other. A unit is analogous to a neuron in the
brain and operates in a similar manner. Each unit translates inputs
into outputs which corresponds to a neuron in a state of either firing
or resting. The processing of information in the network takes place
through the interaction of these units, with each unit sending
excitatory or inhibitory signals to many other units.
This
simple transfer of information is mathematical in nature, rather than
chemical, with the sending of numbers along the connections between
units in the network. These numbers indicate whether a unit is to be
active (fire) or inactive (resting). To indicate the activity level
each unit is associated with an activation value. The activity level of
a unit at any given point in time is its current output. The activity
of the units convey information and determine the temporary physical
state of the network, in the same way that neurons determine the
physical state of the brain through the patterns of their neural
activity.
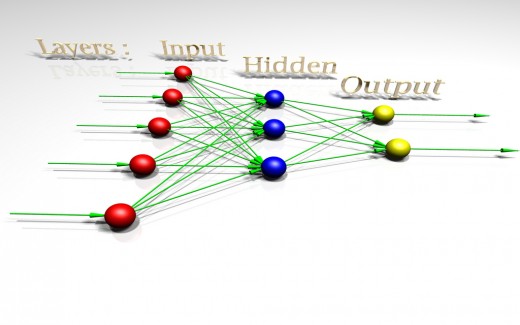
In artificial neural networks the simple,
interconnected units tend to be situated into three basic layers
consisting of input units, output units and hidden units. Input units
receive external inputs such as sensory information and information
from other networks. Output units send information out of the network
which will affect other networks. Each input unit is connected to many
hidden units and each hidden unit is connected to many output units.
Each
unit receives inputs from many other units. These inputs added together
become the net input to the unit. The combined input is modified by a
transfer function. This transfer function can be a threshold function
which will only pass on information, if the combined activity level
reaches a certain level. If this the combined input exceeds a threshold
value, the unit will produce an output. However, if the sum of all the
inputs is less than the threshold, then no output will be produced.
Every
connection between two units has a weight or strength which regulates
the transfer of information between the two units. The weight
determines how much of the output gets through to the unit. This weight
modifies the output of a unit to become the input of the next unit.
Weights correspond to the efficiency of the synapses in the brain and
modify the signals from neurons positively or negatively ie. by making
them excitatory or inhibitory signals. An excitatory signal is one
which attempts to activate (fire) the unit which receives it while an
inhibitory signal is one which attempts to keep the unit from firing.
The greater the numerical value of the weight the greater the effect of
the outputting unit in its attempt to excite or inhibit the receiving
units.
The pattern of the weights between the input, hidden
and output units convey information, represent aspects of knowledge and
determine the more permanent physical state of the network. Information
is stored in the weights and the patterns of connectivity among the
units determine what the network represents. All knowledge then is
contained implicitly in the multitude of weights on the connections
between units.
The combination of weights of each connection in
the network represents then the total physical state of the network.
These weights can be modified with experience and so a unit can change
what it represents through the modification of the strength of existing
connections. Thus a network learns when the connection weights between
the units are modified which corresponds to the brain learning through
the modification of the chemical information through the synapses.
Learning
is accomplished through a learning rule which indicates how the
connection weights must be adapted or changed in response to inputs.
This learning rule indicates whether the value of weights in a network
are to be increased or decreased and such modifications will mean a
change in the total physical state of a network.
CONCLUSION
This article has attempted to describe the fundamental components of a connectionist architecture.
But what are they good for?
Neural networks models can solve the problems of goal-directed learning, of storing motor programs and of producing novel movements. An essential property of neural networks which make them adept for modeling human performance is the networks' ability to learn from experience and adapt to the environment. This means that the network is able to discover solutions to problems, where the solutions are unknown or where there are several solutions to a problem. For example, learning a motor skill.
However, learning occurs very slowly because the weights are gradually changed and fine tuned by a period of training - neural networks learn from being shown examples. Neural networks need to be shown many examples to be able to solve difficult problems. This gradual nature of neural network learning mirrors much human learning which is slow and gradual because expertise takes time and difficult problems require many learning trials.
In another hub I will discuss some of the principle features of neural networks which make them adept at modeling human information-processing