Olber's Paradox for Dummies Like Me

If you grew up not knowing a ton about basic cosmology concepts (like me during the 70s and 80s, for instance, when essentially nobody knew much about the cosmos), or if you just never learned much about the universe in school, you might have looked up and wondered why the night sky isn't unbelievably bright with light from all the stars in the universe. After all, it was assumed by many for centuries that there were an infinite number of stars in the universe, and that the universe was "static and eternal." This means that the universe was believed to have been around literally forever, and it wasn't expanding or contracting.

So why isn't the night sky we observe at night bright as all get-out, completely saturated with photons in every line of sight, as far as the eye can see? Well, we know now that it's because of the expansion of the universe (ever-accelerating) and the finite age of the universe, coupled with the finite age of stars. Back in the early 19th century, though, Heinrich Wilhelm Olbers pointed out that the universe couldn't possibly be static, eternal, and infinite. Let's take a quick look at how he figured that out.

Static. Eternal. Infinite.

Our ancestors had good reasons to assume all of this was true based on their observations at the time. First, the further we peered with our newly invented telescopes (perfected by Galileo, but invented elsewhere), the more stars we kept finding, no matter how far out we looked. The universe certainly seemed to be full of an infinite amount of stars, as far as we could tell.

As for the age of the universe being infinite, we simply didn't have any reason to think otherwise. That the universe had been around forever was one very strong prevailing scientific notion, and to argue otherwise would imply (to many minds) a "moment of creation", and thus a creator.

And for the universe being "static"? This was assumed by virtually everyone - including, famously, Einstein, who included his "cosmological constant" in with his equations on general relativity, later calling the addition of the infamous term his "biggest blunder" - for nearly all of recorded history. It wasn't until Vesto Slipher first, and then Edwin Hubble later on in 1929 announced their findings that the universe itself was expanding, that this thought paradigm began to show cracks. Even when the "static and eternal" concept faced opposition from evidence, in swooped the "Steady State" theory championed by Fred Hoyle (brilliant in his own right, but dead wrong here) to try to explain away the discrepancies the new "Big Bang" theory had brought to bear upon the concept.

All of this sets the tone for Heinrich Wilhelm Olbers, who, in the early 19th century, nearly a century before relativity, and more than a century before the discovery that the universe was, indeed, expanding, concluded one very interesting thing: there's just no way the universe could be static, eternal, and infinite if the night sky wasn't completely bright. Up until the early 20th century, telescopes revealed the universe as simply the Milky Way galaxy, with other "nebulae" (galaxies) as being a smudgy part of our own. The technology just didn't exist to suggest otherwise. Others actually drew the same conclusion as Olbers, including, most famously, Lord Kelvin in the early 19th century, but the paradox bears Olbers' name.

One of the earliest proposed solutions, and, it turns out, the right one, was actually proposed by one of the most famous poets of all time. In 1848, Edgar Allen Poe published his nonfiction essay "Eureka" (1848). Poe wisely called "Eureka" a "prose poem" instead of suggesting that it was a scientific paper of sorts. The paper was, in effect, tantamount to a "thought experiment", as Einstein would later make famous, with 100% deductive reasoning.

Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.

Poe was uncannily prescient in his writing, even though much of it was utter nonsense with no basis in scientific fact. Nevertheless, he foresaw the Big Bang theory by 70 years in "Eureka", and, in doing so, offered one of the earliest resolutions to Olbers' Paradox in recorded history. Not bad for a drug addicted poet!

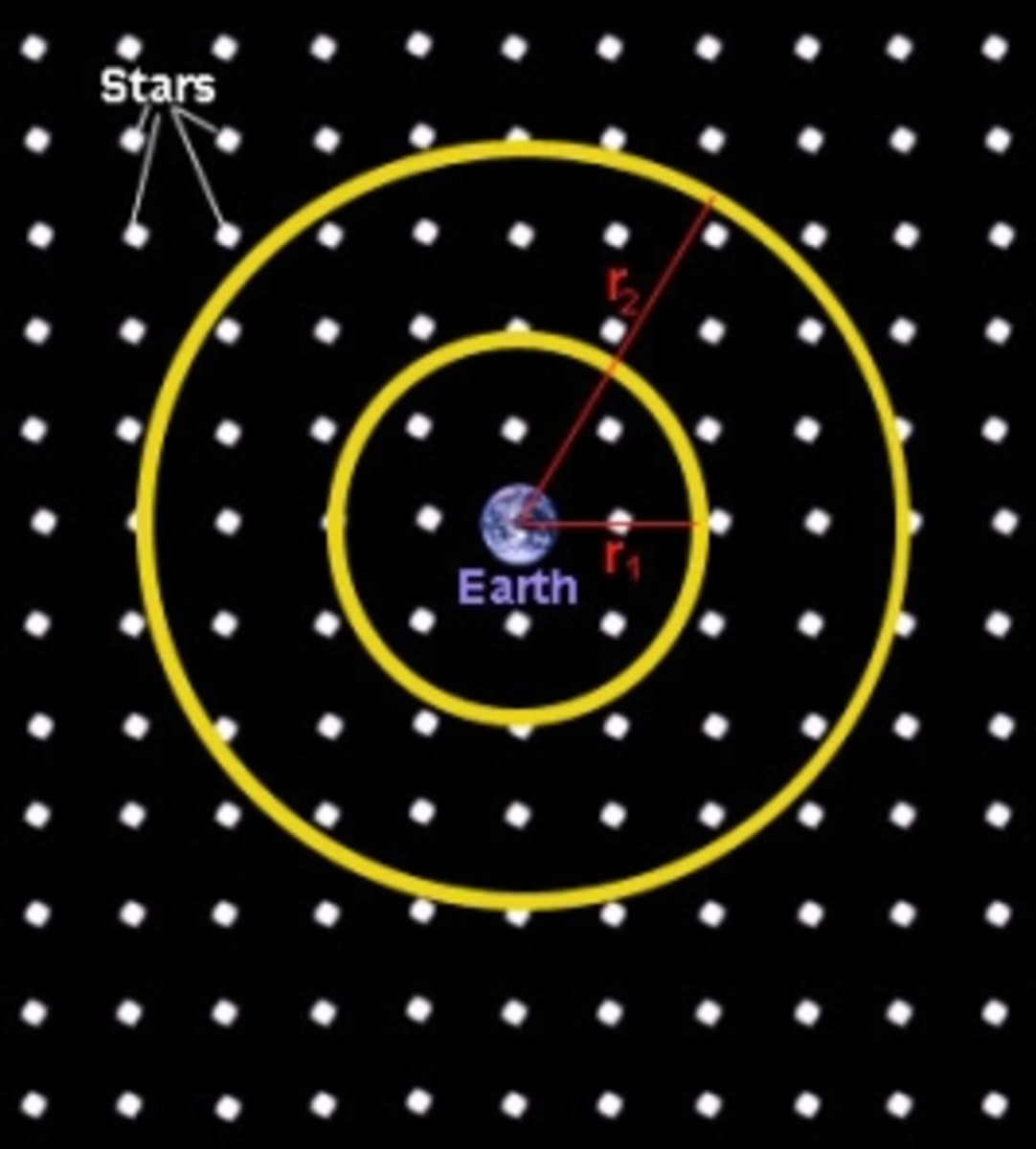
The next time you're having a tough time sleeping at night, think about how this apparent paradox came to be "discovered" in the first place. Imagine peering out into space from a single point (using the earth is fine here; just imagine that it's transparent). From your vantage point, as you look out, you are surrounded by imaginary concentric spheres. The innermost sphere extends out one light year in every direction, and then outside of that, is the very next sphere shell, which contains everything from the outside of the first sphere (radius: one light year), all the way out to 2 light years in one direction (diameter: 4 light years). This continues out into infinity.

Using nothing more than middle school math (or high school geometry), you can determine that there would be four times as many stars in the second sphere, assuming the cosmological principle holds true (that the universe is homogeneous and isotropic). The sphere just beyond that would contain 4 times as many stars as the 2nd sphere, and so on. However, the second shell sphere is twice as far away as the innermost sphere, and so each star would appear four times dimmer than that of the first shell. The distance and brightness cancel each other out, and each shell would be equal in brightness. Obviously, with an infinite number of shells, no matter how small a number you start with in the first one, you are going to end up with infinite brightness in every single direction.

If you want to get really trippy, now imagine the shells drifting outward, and the stars within them doing the same. That's roughly the picture of the universe we have today.