PRICE ELASTICITY OF DEMAND AND HOW IT IS CALCULATED

The law of demand state that, other things being equal, the amount of a product consumers are willing and able to purchase, during some period of time varies inversely with the price of that product. In other words, as price increases, quantity demanded falls and vice versa, other things being equal. Price elasticity of demand is concerned with the extent to which quantity demanded responds to changes in the own price of the commodity. By definition therefore, price elasticity of demand is the degree of responsiveness of quantity demanded of a commodity to changes in the price of that commodity.

It is calculated by dividing the proportionate (percentage) change in quantity demanded by the corresponding proportionate (percentage) change in the commodity’s own price. Using formula:

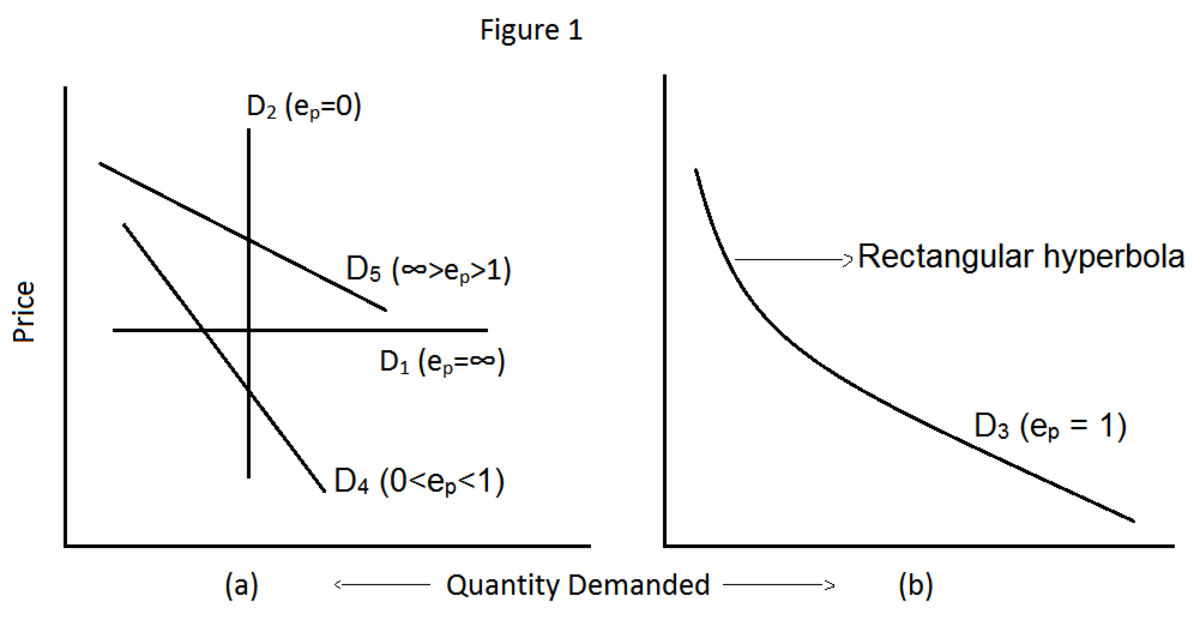
Price elasticity of demand (Ped) = ( ∆Qd /Qd1 ) ÷ ( ∆P/P1 ) where ∆Qd and ∆P are change in quantity demanded and change in price respectively while Qd1 and P1 are initial quantity demanded and initial price respectively. Rearranging, price elasticity of demand, ped = (∆Qd / ∆P) × (P1 / Qd1 ). A calculated value for price elasticity of demand must be negative. This is because of the inverse relationship between price and quantity demanded. When price elasticity of demand is calculated using the above formula, an answer in absolute terms (ignoring the negative sign), and greater than one (1) means the demand for the commodity in question is elastic or fairly elastic. The demand for a product is elastic when a certain percentage change in its price results in a greater percentage change in its quantity demanded. When an absolute value between zero (0 ) and one (1 ) is obtained, it means the demand is inelastic or fairly inelastic. Demand is said to be inelastic for a commodity, when a certain percentage change in price of that product results in a less than a percentage change in quantity demanded.

To illustrate, let us assume two commodities, A and B. Given that price of each commodity was initially $10. Price of both commodities increase to $12, resulting in a drop in quantity demanded of A from 28 to 20. In the case of good B, assume the quantity demanded decreased from 21 to 20.

For commodity A, ∆Qd = 20 – 28 = -8 (new quantity demanded of A minus initial quantity demanded of A) and the corresponding change in price is ∆P = $12 - $10 = $2. Therefore for commodity A,

Ped = (-8/$2) × ($10 / 28 ) = -1.43. By the explanation provided above this result means the demand is elastic for commodity A.

Following the same explanation, for commodity B,

Ped = (-1/$2) × ($10/21) = -0.24. This result, however, means the demand is inelastic. The elasticity values obtained by using the above formula, pertains to calculating price elasticity of demand at particular prices, that is, at their initial prices. In other words, this approach provides price elasticity measure at specific points (not within a range of price change). There is an approach that takes the average of the initial price and the new price as well as the initial quantity demanded and the new quantity demanded. This is the arc elasticity approach. Using this approach, price elasticity of demand formula is:

Ped = (∆Qd /∆P) × (P1 + P2 )/ (Qd1 + Qd2 ) where P2 and Qd2 are new price and new quantity demanded respectively. Using the arc elasticity concept, price elasticity of demand for commodity A is:

Ped = (-8/$2) × ($10 + $12)/( 28 +20 ) = -1.83. The elasticity status of commodity A is still the same i.e. the demand is still elastic and this is normally the case even if the arc elasticity formula is used. This approach has given us additional information that the demand for commodity A is more elastic than we thought. This approach, by taking the average of prices and quantities provide a more reliable measure of elasticity of demand. Therefore unless otherwise requested, the arc elasticity measure is recommended.