Pythagorean Theorem

More Math Hints
What was Pythagoras thinking?
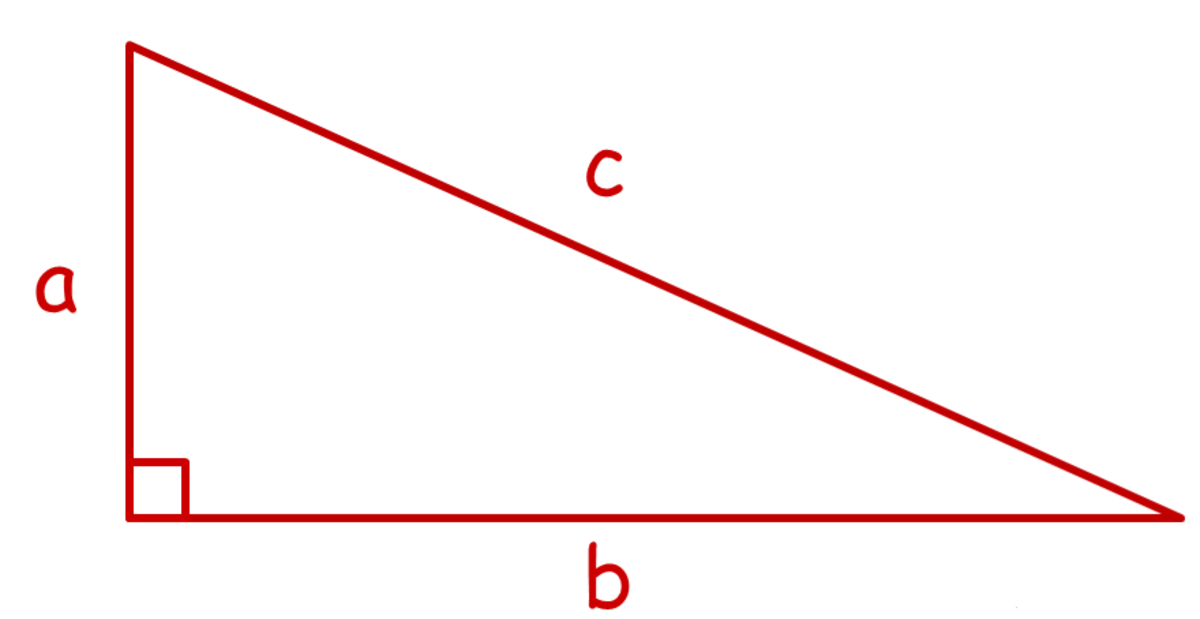
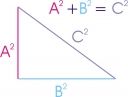
One of the rules you learn in Geometry is the Pythagorean theorem. This states that the sum of the square of the two legs of a right triangle is equal to the square of the hypotenuse.
What exactly does that mean?
Math products from Amazon - Vote for your favorite
What is the Pythagorean Theorem?
Looking at the diagram on the right, you can see a right triangle. The Pythagorean theorem states that if you add the squares of the two legs equal the square of the hypotenuse (the side of the right triangle opposite the right angle -- this would necessarily be the largest side of the triangle).
This means that if you have the lengths of any two sides, you can find the third. For example, you have a right triangle and you know that one legs is 5 and the hypotenuse is 13. You take the formula and substitute in --
step 1 -- 5 squared + B squared = 13 squared
step 2 -- 25 + B squared = 169 --
step 3 -- B squared = 169 - 25
step 4 -- B squared = 144
step 5 -- B= the square root of 144 or 12

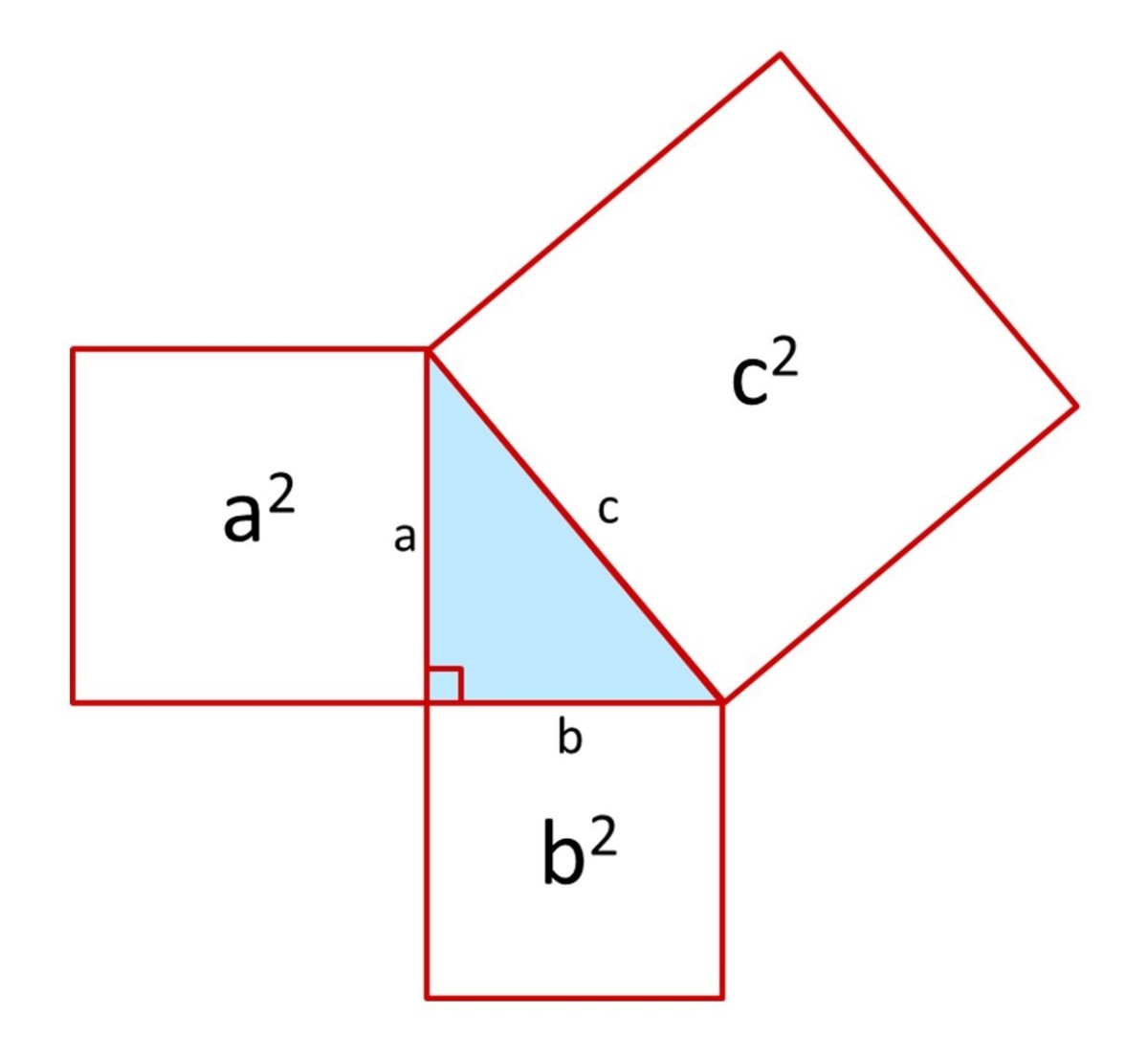
Pythagoras's Diagram
What this theorem represents
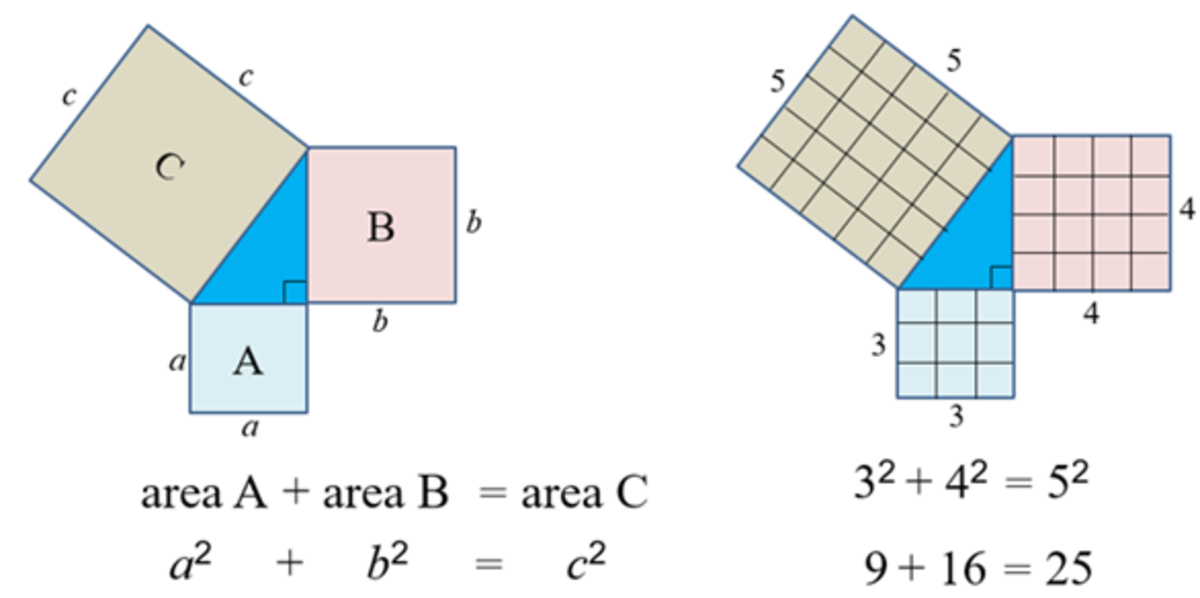
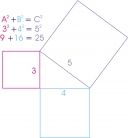
When Pythagoras developed his theorem, he was talking about the area of squares. The diagram at the right represents what Pythagoras meant. He meant that the area of a square with sides the length of one side of a triangle (side A, in magenta, length 3) added to the area of a square with sides the length of the second side of the triangle (side B, in blue, length 4) would add up to the area of a square with sides the length of the hypotenuse (side C, in purple, length 5).
What this means in our example, the area of the magenta square (with a side length of 3 and an area of 3X3 or 9) added to the area of the blue square (with a side length of 4 and an area of 4X4 or 16) equals the area of the hypotenuse (or purple square -- with a side length of 5 and an area of 5X5 or 25). 9+16=25.
This can help you find the length of the third side of a right triangle when you have the other two.

Compugraph Designs Arts Now Site
"Arts Now" is another "Print on Demand" site. They have a nice collection of clocks and watches, including the one pictured here (with math symbols on it). Click on the picture to see the entire math clock collection on the Arts Now site.
Answer this question about math for our fun poll
Which Math subject do you like best?

Compugraph Designs' Printfection Store
In addition to our Cafe Press and Zazzle sites (see modules above), we also have a store on "Printfection" which includes cutting boards (good wedding or housewarming gifts), mugs and cups, tees, etc.
This travel mug only one of several math themed items at our store:
(Click on the picture to go directly to this product's page)
Compugraph Designs' Site on Printpop
I just discovered Printpop -- check out my entire portfolio or click on the graphic to see just this product (called "Black Math"). Check back periodically as new designs are uploaded.