Right Triangle Trigonometry Part 4
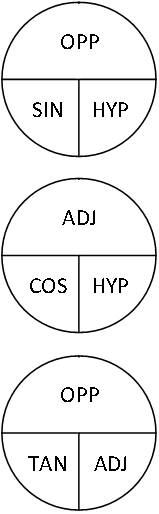
Using Trig Wheels
The examples, so far, have illustrated the process for finding angles given the length of the sides. However, given any two values, the entire triangle can be solved using the trig functions. These “trig wheels” (pictured in Fig.1) are easy to use tools for remembering the functions and how to use given information to solve for unknowns. Each wheel contains an individual trig function, and the process for solving a problem given any two parts of the wheel. The top wheel contains all that is necessary to solve a problem using the sine (SIN) function. Cover the section of the wheel that contains the unknown value; for instance the hypotenuse (HYP). To find the hypotenuse the opposite side must be divided by the value of sine (visually, OPP is over SIN, so divide). If the opposite side needs to be found multiply the value of sine by the hypotenuse (visually, SIN is in line with HYP, so multiply). That’s all there is to it.
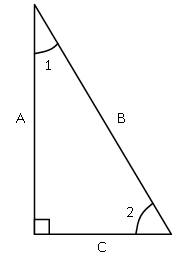
Given the triangle in Fig. 2, use the trig wheels to solve the following two examples.
In this example, if given side A and angle 1, find side B. To solve this, first consider the information. Angle 1 is formed by adjacent side A and the hypotenuse B. The middle trig wheel contains both adjacent (ADJ) and hypotenuse (HYP), so this will be solved using the cosine (COS) function. Side B is the unknown, so covering HYP yields ADJ over COS. To solve this, divide the length of the adjacent side by the cosine of angle 1.
In another example, angle 2 and its adjacent side C are given. Find side A. Since A is the side opposite angle 2, the bottom wheel is used to find the side A. Covering OPP, the unknown side, TAN and ADJ are in line with each other. Solve for side A by multiplying the tangent of angle 2 by the length of side C.