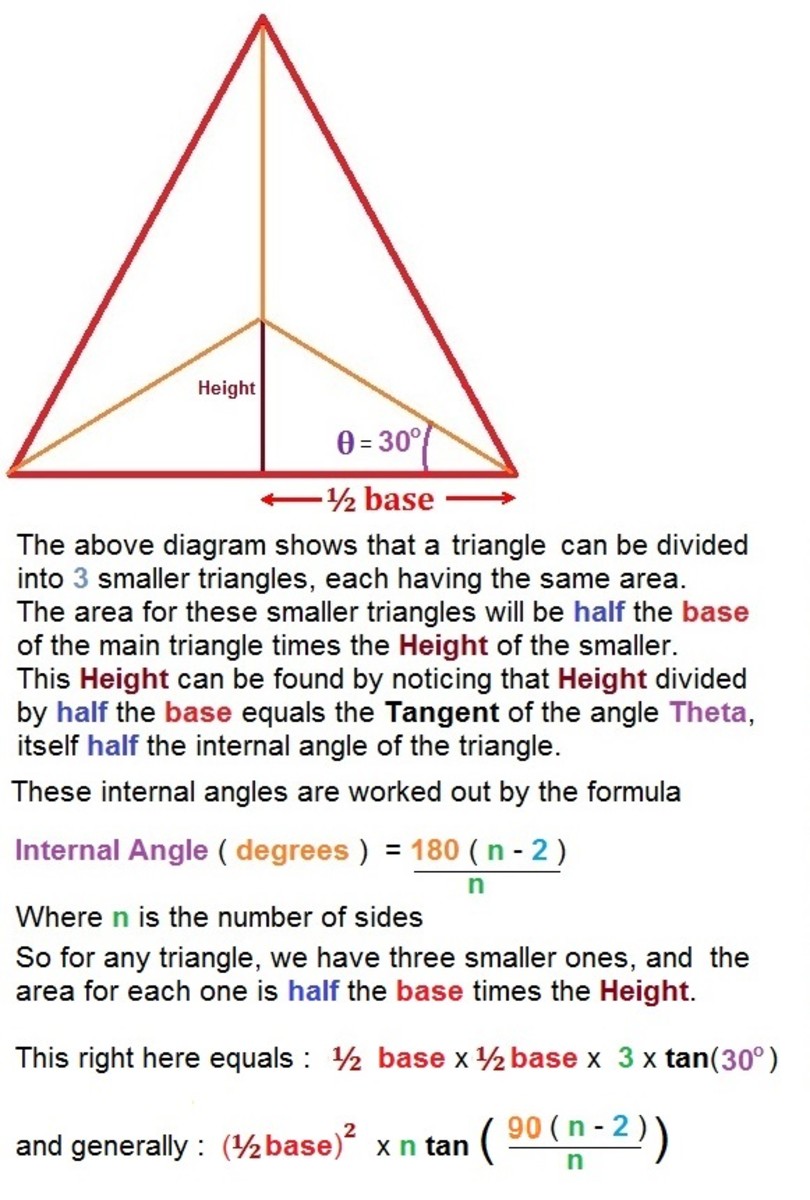
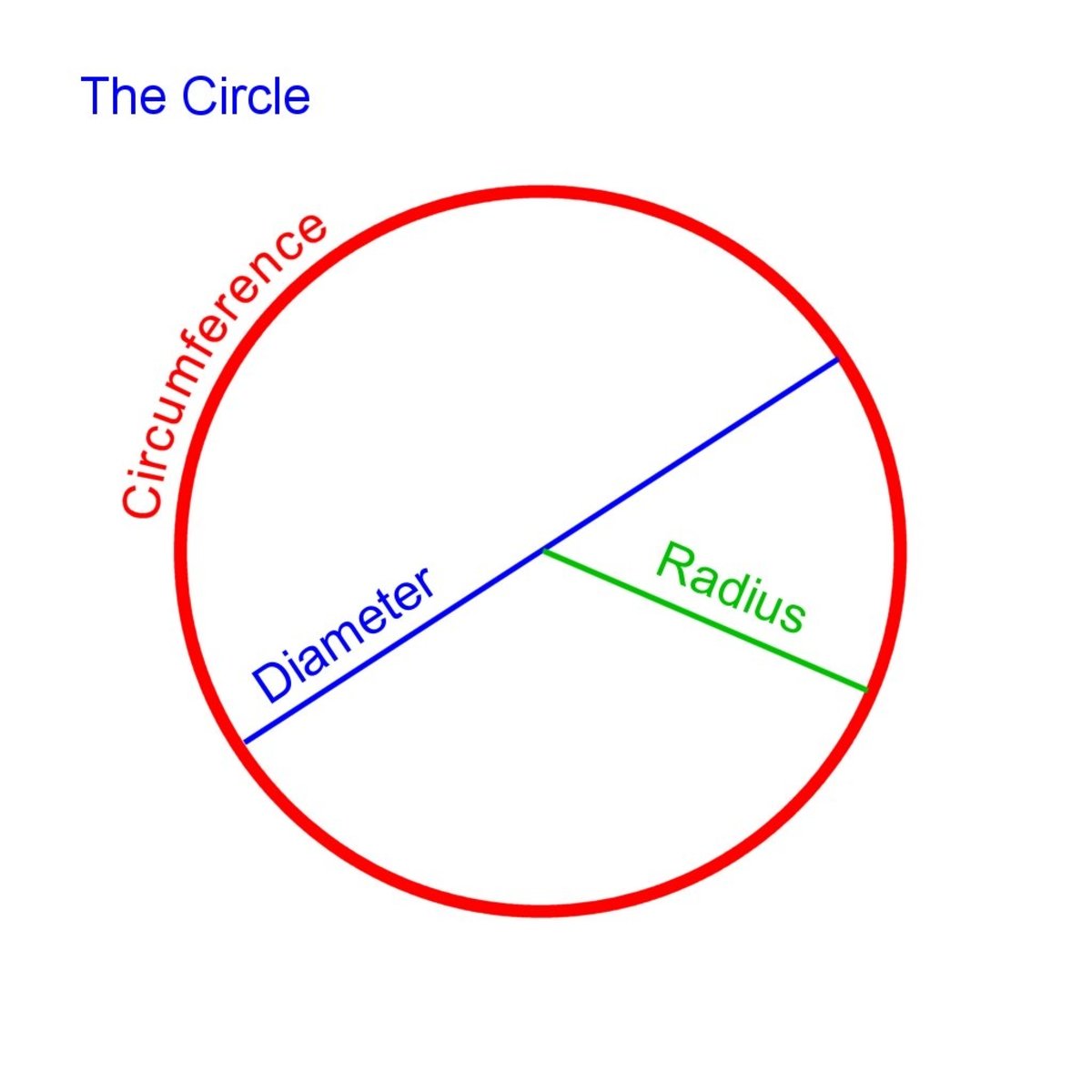
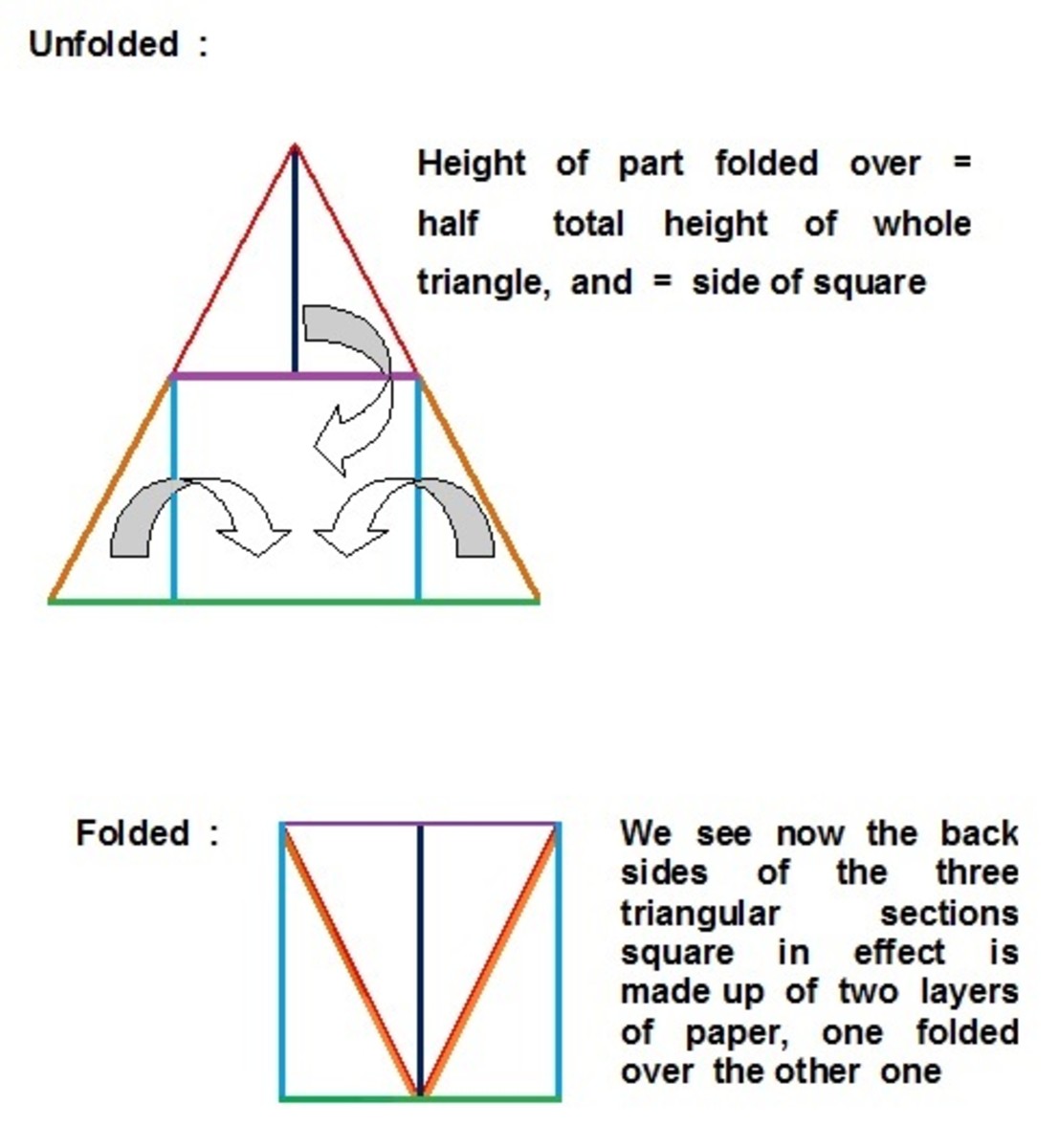
Right Triangle Trigonometry Part 1

Trigonometry
Trigonometry seems to be one of those words better left unspoken. It conjures up images of slide rules, three inch thick textbooks, and countless hours of tedious, complex thought. Trigonometry (trig) merely suffers from bad press. Years of horror stories and whispers in the halls of academia have convinced most people that trigonometry is better left to those with non-existent social lives and too many pocket protectors. Nothing could be further from reality.
Trigonometry is used in many ways, in many fields, and abides by simple laws. Given the right spin, right-triangle trig can be understood by nearly everyone with a good knowledge of fractions and decimals.
Describing a Triangle
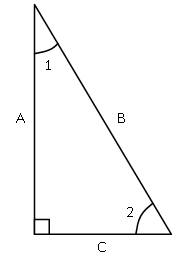
Consider the triangle diagram to the right, and follow along with the description. A triangle comprises three angles, measured in degrees(represented by this symbol ° ), and three sides.
A right-triangle must include one 90° angle; in this case the right angle is formed by the intersection of sides A and C, and is represented by the small box in the corner. Side B is opposite the right angle and is called the hypotenuse.
Angle 1 is formed by sides A and B, and side C is opposite the angle. Similarly, angle 2 is formed by sides B and C, and side A is opposite the angle. Last but not least, the sum of the angles of a triangle must total 180°.
That covers the basic vocabulary and description of a right-triangle.
Mathematical Relationships and Trigonometry
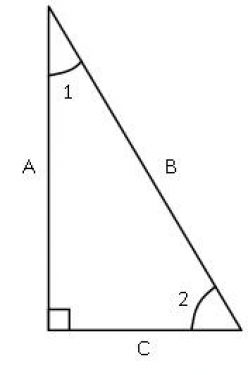
Trig describes the mathematical relationship between all parts of the triangle. There are three basic relationships. These three relationships are described by ratios (sine, cosine and tangent). Ratios compare one element to another. For example, if side B is twice as long as side C, the ratio could be described as 2:1 (B:C or B/C). That merely reflects the fact that no matter what length side B is, side C will always be half the length. If side B is 6, side C is 3. If side C is 5, side B is 10 and so on. Given the characteristics of the right-triangle, relationships between sides and angles can also be defined with ratios.
Using the example above, if the ratio of the lengths of B:C is 2:1; there will be only one angle to yield this result. Stated another way; if the angle is larger or smaller the ratio of the two sides will change. To illustrate this, imagine changing angle 2, formed by sides B and C, while maintaining the right angle. Side B will have to change length, while C remains the same. The only way this can happen is to change the ratio. A similar relationship exists between angle 1 and sides B and C. If angle 1 changes, while maintaining the right angle, then the ratio between B and C will have to change.
Consider the ratios from the perspective of angles 1 and 2, remembering that the third angle will remain constant at 90°. Angles 1 and 2 can be described by the ratios between any two sides of the triangle: A:B, A:C, or B:C. This is where the trigonometric functions come into play.