Hardest Sudoku Ever
My solving technique
I do not try to memorize all those fish, xyz's, flowers or any other names. Read that most of those names are just some form of ALS's and AIC's and a few other tools. A bi-value cell is an ALS. Two or three of them make up the ZY-Z wings. Solving is about as much as what can't go in a cell as finding what can. Strong linked numbers, as pairs, are the hardest to separate. Any weak linked # that sees itself in both of the strong linked pair is gone. I substitute # as short hand for "number", And I prefer to use "number" instead of the common word "candidate". Meaning I use "#" instead of typing "candidate" a hundred or so times.
Have read, and believe from experience, that the key to solving is the use of bi-value cells and some help from larger ALS's. Also read that a lot of the sites don't use the ALS's and are stuck trying to find all those fishy things. I have solved a few of those they said are unsolvable. Because they contained no fish or blossoms or whatever. If they had learned the ALS and AIC basics they may have had more success.
You will see I use 1 thru. 9 in rows, columns and boxes. It is much easier to follow examples when using numbers. Instead of: r5c5 I just say 5-5. Worst yet is SE5. Let me see! S is south and is down and E is right and 5 is the fifth cell. If I want you to look in a box I will say "box 5" instead of in the "center box" or box 3 instead of NE box. Lets see! N is top and E means the right. See, It is just so much easier to follow numbers.
Free sudoku program
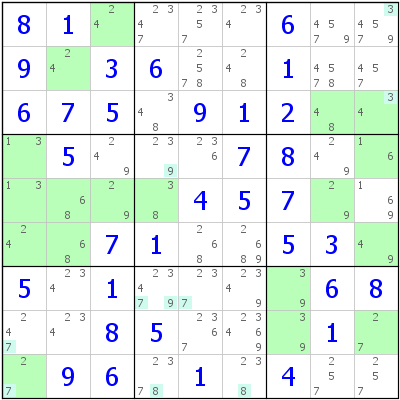
Here is the hardest sudoku, according to conceptspuzzles.com. The site is no longer active. The blue cell at 2-1 is where I did the first solve. I let Sudoku Dragon fill in the possibilities. It is a trial on line sudoku program. I have changed the letter designation for rows and columns to numbers. Will look for another free solver later.
Basic puzzle with possibilities
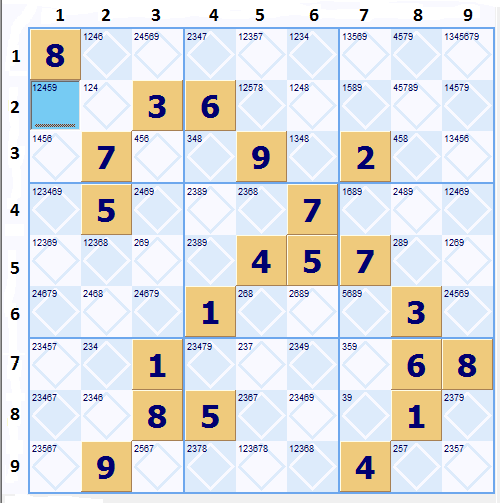
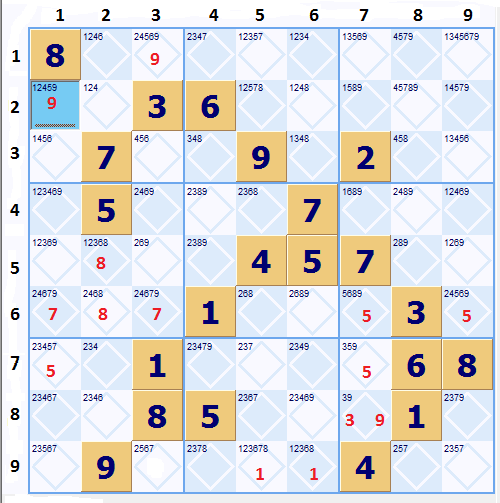
Finding some of the easy stuff
Next is to find any easy singles, bi-value or triples etc. Yielding -->
No singles found. Only one cell having a bi-value and six with strong links between cells. Shown in red.
Then went looking at the few strong links for clues. The 5's in 6-7 and 7-7 I figured would take out the 2 5's at 1-7 and 2-7. One of the rules thwarted that idea. Even though the 5's see two strong links you cannot eliminate them because the strong link has to be between them and not other 5's that are not seen.
Then, maybe I can use the rule. Because if one is on the others are off. I chose not to use it in this case to be on the safe side and not cheat.
The hard part
1. Not seeing much helpful I started looking for ALS. The first one is in the 1st box. #'s 12456 in 4 cells using cell 2-1 as the pivot cell for all #'s that can be eliminated. The pivot cell must have a unique #, That is a # that can not be eliminated. Any cell that does not have at least one unique can not be used as the pivot. The pivot can also be a cell in the ALS. I usually try to find a pivot that is not a part of the ALS's. The other ALS that sees the pivot is along row 2. Containing #'s 1245789 in six cells. You can eliminate 1245 from the pivot. Each of those #'s can see all instances of itself in the ALS's. and since it is not a strong link it is gone. This leaves the 9 as the solution for this cell, All the seven 9's that see it are also gone.
2. After going back over the puzzle I didn't see any easy pickings. Back to searching for ALS's. I decided to concentrate on the bi-value 5's. Finding ALS 2345679 in 6 cells in box 7 and the other along row 7 having #'s 23479. Cell 7-1 is the pivot, 5 is the unique. so, the 2347 are gone because they see all instances of themselves in the ALS's, This makes the 5 as the solution to 7-1. You can eliminate all 5's that see this 5. The 5 at 7-7 can also be isolated. The following is used in tough cases. I try not to use this almost "guessing". Sometimes have to resort to it when really stuck.
"Trials of several kinds finish off puzzles when all other logical tactics are exhausted. Monster puzzles may require a trial generator, producing a small set of trials, one of which must succeed." From: http://sysudoku.com/order-of-battle/
3. One of the 5's is the 5 at 7-7. This causes the 3-9 pair in box 9 leading to a lot of eliminations. Three 3's and five 9's
At this point the solving was easier. It still took effort though.
Flaws in my solving
Trying the ALS technique I used in step 1 and 2 on another hard sudoku did not work. I think it was that there was a 50/50 chance and I just got it right the first time each step. So it was via trial and error more than by ALS's. Bottom line! still solved the puzzle.
More solving
4. 6 is solved for 1-7. ALS: box 3 14578 and col. 7 1568. The 1 and 5 are gone. 6 is left.
5. 6 at 3-1 ALS: row 3 134568, box 1 1245
6. 5 at 1-3 ALS: box 1 124, col. 3 245679
7. 6 at 9-3 ALS: box 7 2347, row 9 257
8. 1 at 1-2 ALS: box 1 124, row 2 234
9. Remove 2 and 3 at 5-2 ALS: col. 2 234, row 5 2389. This removes 3's in box 5 and 7 making things a lot cleaner.
10. Wanting to go back and deal with the 5's. ALS: row 2 124578, col. 7 58 removed the 5 and 8 from 5-2 leaving 1. Making 8 the only # in 4-7. Then 5 only in 6-7.
I have changed programs to HoDoku. The trail has expired on the other and I am trying this one out to compare.
The moderate stuff
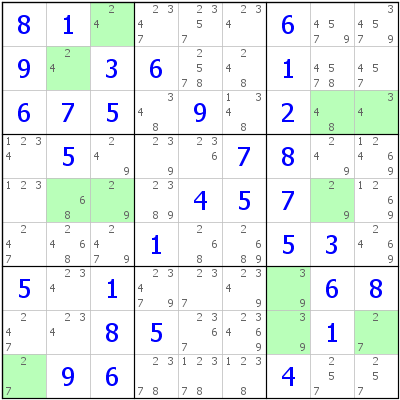
The easy part
Looking around for solves I came to box 3 and found 3,3 in col. 9 and 9,9 in row 1. cell 1-9 now has strong links to 1-8 and 3-9. All other #'s in a bi value strong link can be eliminated.
Have set the bi-value color to be light blue in the HoDoku program. Other color options available.
Found a single 1 in box 3 at 2-6.
1-3 pair and 6-8 pair in box 4
two 7's in box 7, col. 1 lead to removal of 7 in 6-1 leaving the 7 at 6-3
Single 1 in box 8 at 9-5
I left off at 4-4 with a 7-9 bi-value to show the 2,3 and 4 about ready to be removed.
The rest of the sudoku is now easy to solve.
Easy part