R is for Rocket - Mass Optimization

Mass and Altitude
Most of us have taken some sort of basic science course in school where they taught us Newton's Law. That's the one that uses the formula F = ma and says the acceleration of an object is proportional to the force applied and inversely proportional to the mass. In other words, the lighter something is, the faster it accelerates under the influence of an external force. It's not surprise therefore that in model rocketry the first impulse a designer may have would be to reduce the mass as much as reasonably possible. This would mean there's less rocket for the motor to push on and it would therefore accelerate quicker, reach a higher top speed and a higher altitude. Well, unfortunately that's not how it works. No, I'm not saying that the laws of physics don't apply to model rocketry. Rather, I'm saying the relationship between the mass of your rocket and its apogee (the highest altitude it can reach) amounts to much more than a simple application of Newton's laws. This is why the notion of mass "optimization" exists at all. Otherwise we'd just try to make rockets with zero mass all the time and there wouldn't be any optimization about that.
What's Wrong With a Light Rocket?
Nothing's wrong with a light rocket. You're more likely to make a rocket that's too heavy than one that's too light, just trying to get the stability of the rocket in check. As you'll learn in my other hub about stability, there is a delicate balance between center of mass and center of pressure that must be maintained so that the rocket flies straight and unless you are lucky or very experienced, you'll need to move mass or add mass to your rocket to stabilize it. Your rocket may already be a bit overweight because of this, depending on how much it took to get it stable. That's not taking into account any payloads or electronics or what have you.
The problem is, you don't want a rocket that is "too light". That means there's a perfect mass for every rocket. What's too light and why is a light rocket not going to fly as high as a heavier one? Well let's look at what happens if you launch a rocket with a mass of 1 gram!
A Small Case Study
So you've got a rocket that weighs 1 gram. Congratulations, that's damn near impossible but I'm exaggerating here to prove a point. So let's say we cram a C6 class engine into this 1 gram rocket (and ignore the fact that the motor has mass itself). A C class Estes motor has an impulse of about 8.8 N-s and an average thrust of about 6N, hence the 6 in the designation. For the sake of simplicity let's assume the motor produces constant thrust of 6N throughout the burn (which it doesn't). The calculation is simple. One gram is 0.001 kg so F = ma becomes 6 = 0.001a. Solving for a gives you a = 6000 m/s^2. You have to subtract gravity which is 10m/s^2 so the acceleration is really 5990m/s^2. Now since the motor burns for 1.9 seconds, you have v = at = 5990 x 1.9 = 11381 m/s. That's the speed of the rocket at burnout. Oh by the way, just in case you're interested, this value is almost exactly the escape velocity for Earth. So in 2 seconds your $3 motor has accelerated your 1 gram rocket to the escape velocity of Earth, meaning there is no max altitude. It will leave the planet's gravitational field and drift in space forever.
Sure I chose a ridiculous mass of 1 gram but it's not THAT far off from reality and the astute among you should be raising an eyebrow because clearly there's something wrong with this calculation. What's wrong with it is I didn't include aerodynamic drag in the calculation! What's the formula for that? Well it's rather complicated but the most simplistic version is F = 1/2 x Cd x ro x A x V^2, where Cd is the drag coefficient, ro is your air density, A is the cross sectional area that the oncoming airstream sees and V is the velocity of your rocket. Let's make up some values so the equation yields a number for our 1 gram rocket. I'm going to make Cd 0.2, which is very good for any rocket, A will be 0.000314159 m^2, based on a 2cm diameter body tube (I'm including the fins in this area), ro is about 1.2 and V is our velocity at burnout of 11381 m/s. The drag force therefore, at burnout, would be F = 0.5 x 1.2 x 0.2 x 0.000314159 x 11381^2, which is equal to 4883 N. I mean just look at that number! I chose very favorable values for the drag coefficient and area and it still gave me a drag force of almost 5 kilonewtons! If you were surprised that our 1 gram rocket could reach escape velocity in 2 seconds with only 6 N of thrust, imagine how quickly it will STOP DEAD with 5 kN acting against it. This is all assuming the rocket doesn't disintegrate or burn up, which it would at the speeds and forces we're talking about.
The moral of the story here is, making a rocket extremely light will not only net you LESS altitude due to air drag but it takes considerably more fuel and thrust to move something so light because it has virtually no inertia and cannot absorb the motive power being imparted by the motor. The motor is basically being wasted. Imagine trying to fire a feather out of a high powered rifle. You can put as much gunpowder as you want behind that feather and it will leave the muzzle of the gun at tremendous speed but it will come to a halt only a couple of feet in front of the gun every time because all the thrust in the world is no match for air drag, which increases quadratically with velocity.
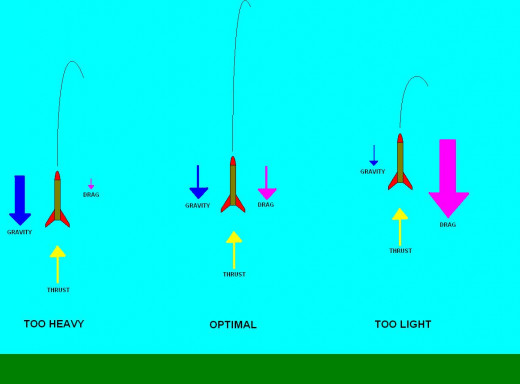
Mass Optimization
Altitude is achieved by a trade-off between thrust and drag. On the one hand, lighter models will reach higher top speeds more rapidly and will thus go higher. On the other hand lighter models will experience higher drag forces and will therefore NOT go higher. As one reduces rocket mass, you will see the thrust component of altitude increase, the drag component of altitude decrease and where the lines intersect there is a theoretical perfect mass at which the best altitude can be achieved. At this mass, the model rocket is light enough to be propelled easily by the motor and heavy enough to plow through the air for some time without losing too much speed after the thrust is gone. Every rocket will have a different "best mass" because every rocket will have either a different motor or a different drag characteristic or both. Only by calculating both for a given design will tell you what mass is best. This sort of work is best done by a computer program because it often comes down to recursive math that iterates different masses and checks the max altitude each time to converge on a solution. Trying to interpolate some sort of a formula for this is time consuming and unnecessary since it'll only change with every new rocket or even if you make the slightest modification to an existing rocket.
The light rockets accelerate instantaneously but have very short flights
A Rough Approximation For Best Mass
There's a rough approximation you can use to figure out the best mass for your rocket. It's not very precise but it will surely get you in the ballpark! It involves performing an energy balance. You see the motor imparts its energy to the rocket in the form of speed. The air imparts energy to the rocket in the form of drag because it takes energy to displace air around a rocket. Therefore what you want to do is continue to decrease mass, little bit at a time and calculate the thrust and drag energies. What you'll notice is that with decreasing mass, your velocity and therefore kinetic energy will rise but your drag energy will rise faster because it depends on v^2. When your drag energy becomes greater than your thrust energy, you take THAT mass as the best mass because any lighter and the gains in kinetic energy will be cancelled out by the drag and then some. Here's how you would do this:
Power (a form of energy) is F x v. You'll calculate this both for thrust and for drag.
Step 1: Pick a mass to start with, say 50 grams or 0.05kg.
Step 2: Start with thrust. Use the average thrust that the motor is rated for and throw it into F = ma, solving for a
Step 3: Solve V = at where t is the duration of the motor's burn. You'll have to look this up on ThrustCurve.org. You will now know the velocity of the rocket at burnout
Step 4: Solve F x v using the velocity you just calculate and the average thrust
Step 5: Now let's work on drag. Calculate F = 1/2 (Cd) (ro) A V^2. Use 0.5 for Cd, 1.2 for ro and you'll need to calculate A by calculating the area of the circle for your body tube and whatever rectangular area is contributed by the fins. Do everything in meters so the math doesn't screw up from incompatible units.
Step 6: Solve F x v again using the F for drag this time and the velocity from Step 3.
Step 7: Compare the P values from steps 4 and 6. If Thrust P is greater than Drag P, reduce the mass by 5 grams or whatever you decide to increment by and try again. Stop when the numbers are about equal.
Notice the lower acceleration but longer coast of the heavier rocket
In our earlier example with the 1 gram rocket the Thrust P would have been P = 6 x 11381 = 68286 and drag P would have been 55573423, which is way too high. A much better mass in this case would be 30 grams, which is still a little too light but not by much. Your thrust and drag powers would be 2280 and 5168 watts respectively. Feel free to play with the numbers until you determine exactly what the mass ought to be for this rocket and always remember that your own rocket will have a different best mass because even if it uses the same motor, the area will more than likely be different.
Rockets Are Like People In Many Ways
If you want to play football you want a perfect balance of weight and speed so that you don't crumple when someone hits you but also can run fast enough not to get hit in the first place. Furthermore the human body has a lot of "non-functional" bulk simply to hold things together well and provide ample reserves for us to stay healthy, even when food is scarce. While this has nothing to do with model rocketry, your rocket benefits from an ideal weight in the same way humans do... sometimes for the same reasons, as in the football example. The rocket needs to be beefy enough to push the air out of the way and not get slowed down, like a football player pushes people out of the way, hopefully without getting slowed down but your rocket needs to be light enough that the motor can accelerate it with easy, just like a football player needs to be light enough that his legs can move him quickly into the end zone.
Since model rocketry involves many trade-offs, as you'll discover, it's not so trivial to know when to deal with the issue of mass. Should you define it before you begin building or after? Well that's a tough one because with the best of intentions, sometimes your rocket will need adjustment and this might throw off your mass. I don't think it hurts however to do the calculation in advance so that you are at least aware of how far off the mark you are, as you build your rocket. This way you at least know early on whether you need to add or subtract mass and can sometimes make changes in time to perfect your rocket on the fly.
Think of the runner's legs as THRUST and the other players as DRAG. Who's going to make it to the end zone? What about someone in between?