Great Word Puzzles for Tiger Moms and Their Cubs: a Tricky Word Matrix Puzzle and Solution #1
A word matrix (aka Word Bingo) is a word puzzle in which you must place twenty-five listed words in the 5-space x 5-space grid in such a way that the words in each column, in each row, and along each diagonal have one letter in common with one another. The common letter will be different for each row, column, and diagonal. In other words, there will be twelve different letters that are used as common letters: one for each of the five columns; one for each of the five rows, and one for each of the two diagonals.
This type of puzzle uses observation and logic – rather than actual verbal skills – much in the same way that a Sudoku puzzle uses numbers as symbols in a logic puzzle, but does not actually use skills of arithmetic.
The puzzle printed here (as a picture which can be printed out) has some features that are designed to help you in using your logic. Two words from the list are included in their correct spaces in the matrix, to give you a jump-start. The boxes around the outside of the grid ("matrix") are available for you to write the letter that you have figured to be the common letter of that column, row, or diagonal. The alphabet below the grid is present to use in identifying certain features of the words and letters, which you may discover as you ask yourself the helpful questions listed below.

Great Gifts for Tiger Moms and Their Cubs
Questions for Starting Off
1) Are there any spaces on the grid where every letter of its word (four letters) must be found in all the other words around it? Where is that space (or spaces)?
2) How many letters of a word (in most spaces on the grid) must be the same as in the words around it? Is the number the same for all spaces on the matrix?
3) What is the minimum number of times any letter of the alphabet must appear in the words on the word list, in order for it to be the "common letter" of a row, column, or diagonal?
4) How might you be able to figure out which twelve letters of the alphabet will be the common letters for this particular matrix?
5) Will it probably be easier to locate the correct space in the matrix for words that use two, or three, or four common letters? Which will be the most helpful?
6) Which word should probably be found first, in order to start figuring out the common letters and locations of all the other words? How might you be able to figure out that word – or the letters in it?
7) What happens if one letter of the alphabet is used more than the minimum number of times in the word list? Will that make it easier or harder to figure out where a word goes? What other information can that help you to see?

More Tiger Gifts to Give and Request
First the tips, in the form of answers to the questions above.
1) The center space (row three, column three) has to have a letter in common with its row, its column, and both diagonals. Therefore, all four of its letters must be "common letters."
2) The majority of the words (16) need to have only two letters in common with others. Eight words, the ones in the corners and along the diagonals surrounding the center space, must have three "common letters."
3) A letter of the alphabet must appear in at least five different words in order for it to be a common letter, because there are five spaces in any column or row or on either diagonal.
4) In this matrix, there are exactly twelve letters of the alphabet that are used in five or more words (and no more than twelve). There are two ways to find them. One is to make an actual count of letters, by placing a tally mark below the letter in the printed alphabet, as you read off each word in the word list. This can take a little time and can be tedious, but it can be helpful.
A shorter version of the same process would be to quickly scan ("eyeball") the word list to see which letters seem to be the most common, and then make an actual count of them. Next to each of those letters in the alphabet, write the number of times it appears in the word list. Don't always assume (in other Word Matrix puzzles) that there will be exactly twelve letters that are used in five or more words, because one day you might be unpleasantly surprised!
5) In most word matrices, there will be only one word that fits as the center word, using four common letters, and since there is only one possibility, it will probably be easiest to find and know with certainty that that word is correct. There may be other words in the list that use four common letters, but they will not fit with the two words that are pre-printed in the puzzle. Finding the center word will make solving the rest of the puzzle much easier.
6) A good way to find that center word is to go through the list of words and compare it with the common letters you have discovered. Mark all the words that contain four common letters. Then check those words against the two pre-printed words in the grid. Remember that the center word will have to have at least one common letter with each of those two words, because of being in the third row and because of being along the "7:05" ("SW-NE") diagonal.
7) Some letters may appear in the word list more than five times. That simply means that they will also appear in other spaces in the grid in addition to the five spaces where they appear as a common letter. It will probably mean that other common letters of certain words or columns will have to be identified or placed before they can be.

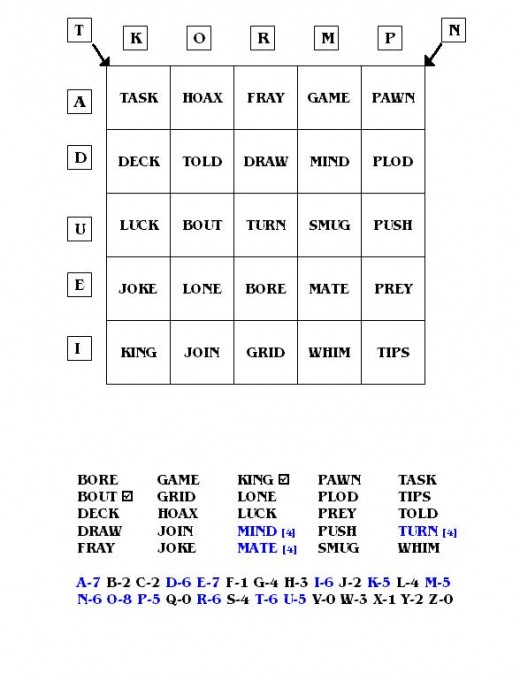
If you find that you need more details about how this particular matrix was solved, please feel free to send me a note through the contact button on my profile, and I will be happy to provide a step-by-step solution.
Comments about this article and puzzle are welcome, even if you are not a signed-in member of the HubPages community.
In the meantime, Happy Puzzling!