- HubPages»
- Books, Literature, and Writing»
- Commercial & Creative Writing»
- Creative Writing
Zeno in the Classroom
zeno
It is never easy for a teacher to teach mathematics. Students instinctively recoil in fear, disgust or apathy at the mere mention of the subject. Indeed, anyone foolhardy enough to mention to their friends that math is not that bad -that in fact, they actually like doing Algebra- will find themselves asked very quickly to return to the alien planet which had spawned them. Lessons have to be interesting and easy for them to understand. Admittedly, I cannot always satisfy either or both criteria. The following episode, however, remains one of the happier memories a teacher can claim as their reward for being overworked and underpaid.
The lesson began with the simple instruction, "I want you to think carefully before replying."
"If I said to you I am a liar-" I commenced.
"We know you are, Mr Ekbar," Daniel interrupted with a grin. "My math report proves it."
"Daniel, please go to the arena. The lions are waiting for you," I was goaded to reply. This brought appreciative laughter and cries of "Go, sir!"
"If I said to you I am a liar, am I telling the truth?"
"Yes, er, no, I mean yes, I think, maybe," Francesca vacillated, furrowing her brows in concentration.
"You've certainly made up your mind, Francesca," I asked wryly. "Anyone else?"
Helda offered a critical response. "If you are a liar, then your statement ‘I am liar' is not true. This makes ‘I am a liar' to mean ‘I am not a liar'. Therefore you must be telling the truth."
A round of applause followed as my invitation to acknowledge the alleged success of Helda's Socratic Method.
Wendy, however, was pensive. She proposed a corollary to Helda's analysis. "But if Mr Ekbar is now telling the truth, then it was true when he said ‘I am a liar' and we're back where we started."
At this point Jimmy forfeited his membership of the society of natural philosophers. He didn't want to play the game any longer. "I have a headache, sir. Truths are lies and lies are truths. Something's wrong somewhere."
He rested his head resignedly on the desk.
"Exactly, Jimmy," I agreed consolingly. "We are chasing our tail." I offered clarification. "What we have is a paradox; a statement that contradicts itself. Here's one you may know. The irresistible force meets the immovable object."
"I know that one," Stavros informed us. "It's like your big brother threatening you to do his chores just when you are getting ready to watch the Super Bowl championship game on TV."
"I'm not scared of my brother," Chris boasted irrelevantly. He was rebuked by calls of liar' by his friends.
"This leads us to a series of paradoxes first proposed by the Greek philosopher Zeno, born in Italy about two and a half thousand years ago."
"Hey," Jimmy protested emphatically as he raised his head from the desk, "How could he be Greek if he was born in Italy?"
I tried unsuccessfully to clarify the situation. "He was born in Southern Italy, which at the time was a Greek colony."
"Now you say Italy is Greece and Greece is Italy!" Jimmy wailed before lowering his head again onto the desk.
"That is a paradox in itself," Janice spoke, believing her comment was an epiphany.
"Okay, I need an assistant," I remarked. Steve's hand was up first. "Good. Steve, go to the corner. Now, I'm going to prove to all of you that Steve is incapable of walking to the other side of the room."
"Only if you break his legs, sir," Alex called out gratuitously.
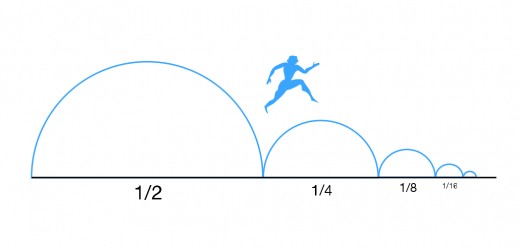
"The room is about twenty feet in length, right?" I asked, soliciting agreement. I waited for nodding heads before continuing. "Before Steve can reach the other side, he must first reach the ten foot half way point, correct?" More head shaking followed. "But before he can reach half way, Steve has to get a quarter of the way, which is two and a half feet from the start. Are you still with me?" I wanted to know. This time heads were motionless but I knew brains were thinking by the dazed expression on every face. "And to make it a quarter of the way through, Steve must first walk one and one quarter feet to reach one eighth of the required distance, but before that he must get to one sixteenth of the way, and so on." I paused to catch my breath and to allow my minions to assimilate the data. "We are halving an infinite number of times," I stated as I prepared for my punch line. "And since infinity never finishes, Steve will never be able to take that first step."
Steve pretended he was trying to break free from his invisible leg shackles.
Yao encapsulated everyone's puzzlement by exclaiming, "That's weird!"
To allay her concerns I asked, "What is the flaw in Zeno's method of bisection?"
"What does bisection mean?" Janice asked as a distraction.
"Maybe they didn't have fractions in ancient times," Lino offered simplistically.
"It depends on the units they used," was another naive hypothesis.
In exasperation and to obtain absolution for my incompetent teaching I pleaded, "Helda, what do you think?"
"If you halve something an infinite number of times, sooner or later you will get to the end," she argued convincingly. Her sophistry was persuasive but incorrect.
Jimmy raised his head and completed the puzzle. "When you add fractions together, you always get an answer."
"Precisely," I responded. "Zeno assumed that the sum of the infinite sequence in our case - is limitless, but in fact, it has a sum of 20, which is the length of our room."
To visualise the idea of a limit, I got each student to measure a length from one wall and to stand on the chalk line marking their endpoint. Steve measured 10 feet, Helda was assigned 5 feet, and so on. It quickly became clear that by the time the seventh person, Jimmy, had to take his position, he was required to be about 8 inches from his neighbour, and the eighth person was expected to stand no more than 3 inches from Jimmy. In fact, students were now required to be so close together that they believed that they could physically merge into one another if they pushed each other hard enough. Some even pretended they were playing a game of Twister! At one point the pushing created a snapshot moment when the group resembled Joe Rosenthal's famous World War 2 photo, Raising the Flag on Iwo Jima. They finally fell to the ground laughing.
I knew then that I had reached my limit of professional satisfaction.






