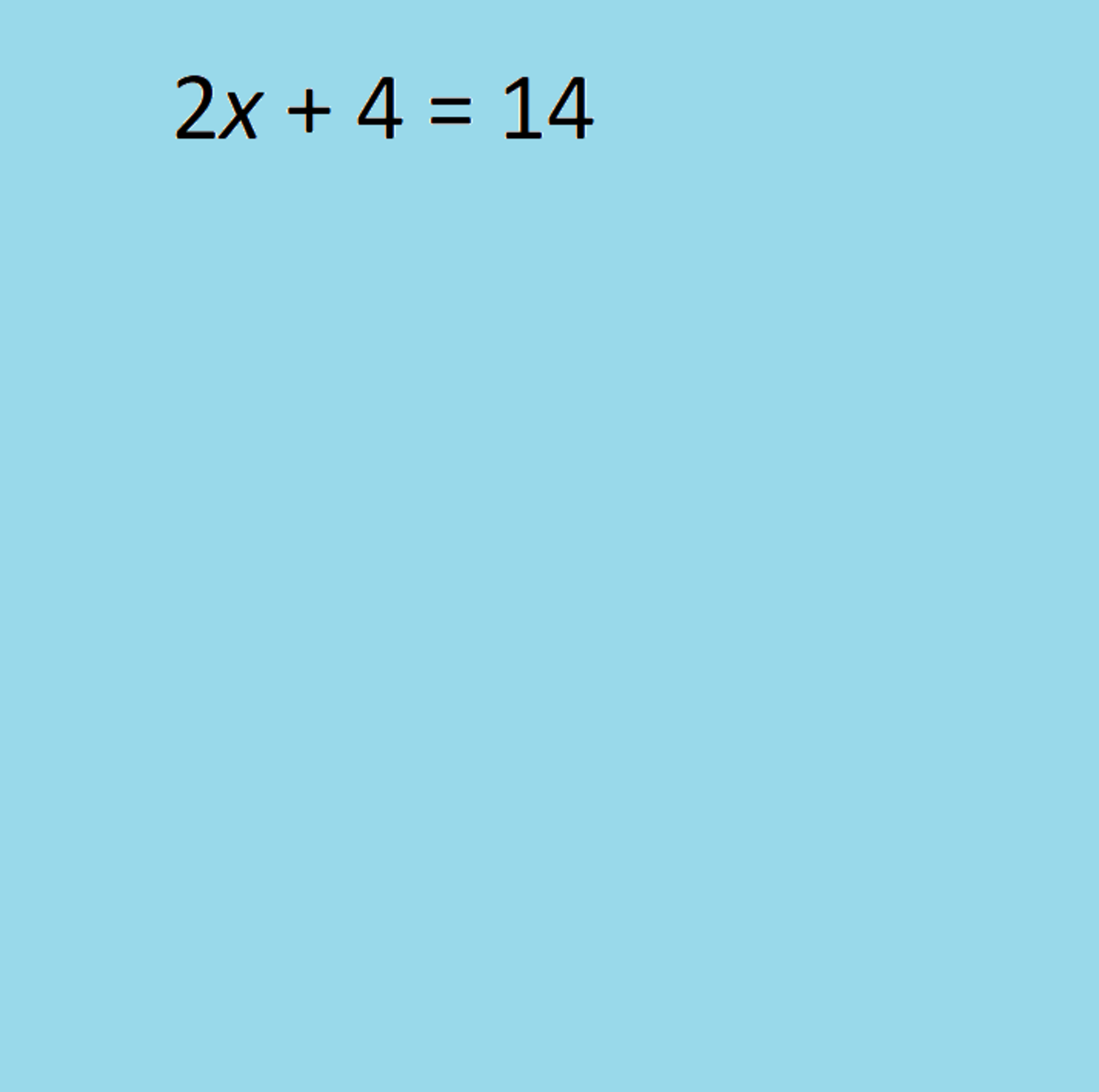Compounding Interest - What Is It and Why Do You Want It?

The general concept of compounding interest is fairly simple. As an example, we will look at Jamie who is 20 years old and has $500 that she received for her birthday. Now, she could put that money in a secret safe for a rainy day, spend it on a new wardrobe, or invest it. I’m sure you already caught on to which option is best supported by finance specialists; invest it! But, wait a minute; why not save it for a rainy day? Well, the answer is simple. Saving your money is great and it keeps you prepared, however, you will only ever have what you put in. If you invest your money, you can get back more than what you put in and with compounding interest, you can get a lot more than what you originally put in.

So, Jamie decides to take her $500 and invest into a financial product that offers compounding interest (we will talk about those options later in this article). If the interest on her investment is only 1.5% and she doesn’t touch that money for 45 years (until she is 65 and ready to retire), her $500 will turn into $977.11! And that’s if she doesn’t add more to invest. Let’s look at how this works and why $500 can “magically” turn into $977.11.

Sorry guys, but there is going to be math involved today. However, don’t freak out because if math isn’t your strong suit, then there are free online calculators that can do the math for you.

The equation for compounding interest is:

FV_n = PV(1+i)ⁿ

Now, let’s look into what each variable means:

• FV_n: This variable represents Future Value for the number of periods that you want to look at. Basically, this equation solves for how much money you will make on compounding interest.
• PV: Present Value implies exactly what it sounds like – the current amount of money you have – but also, PV represents the original value you invested. Don’t overthink that too much. Just look at it as your starting amount.
• i: This variable is the interest rate that you are analyzing.
• n: The number of periods that you are analyzing.

If we want to look at this generally, then “n” would be the number of years that the investment will be gaining interest. However, not all products compound annually. There are some that compound quarterly, monthly, bi-annually, and even daily. So, with that in mind, don’t look at “n” as the number of years but rather, the number of times your investment will gain compounding interest

Still Confused?

If the interest is compounded annually and you want to know how much you will have in 2 years, then “n” will equal 2. However, if the interest is compounded every month and you want to know how much you will have in 2 years, you will multiply 2 by 12 (12 months in a year and compounding occurs every month). So, for monthly compounding for 2 years, “n” will equal 24.

Now that you understand the equation, let’s look back at Jamie. If we were to apply her information to the equation the variables would look like this:

• PV = $500
• i= 1.5% (or .015)
• n = 45

And when we plug in those variables we should see this: FV₄₅ = 500(1+.015)⁴⁵. And once again, what does this equation tell us? It tells us that we are looking to find how much $500 can turn into if we gain a 1.5% compounding interest rate for 45 years. The answer, as stated before in this article, is $977.11.

Jamie only invested $500 one time and never added more to the fund she had money saved in. Regardless, she saw a nice gain of $477.11 and that is almost double the amount she invested. So, what does this have to do with you? Well, as an individual you can see how beneficial it is to start investing early and how wonderful compounding interest can be. As an advisor or planner, this information is important to provide to your clients so that they can save money and plan for retirement or a large upcoming expense. You can see that even with a small initial investment, you can still take home significant gains. If Jaime had added more money as she went along, she could have had even greater returns. So, what the heck are you waiting for? Oh, you may want to know what investment products offer compounding interest.

The main two options for investing in funds that offer compounding interest are savings accounts and certificates of deposit (CDs). CDs will usually have higher interest rates, however, there is a penalty for withdrawing money prior to maturity. Savings accounts typically have low interest rates, but you can take the money out at any time. Bonds are also an option, however, it’s not as common and bonds will typically have a much longer maturity. Banks offer information about interest rates and minimum investment amounts on their websites so make sure to shop around before you make a final decision.