Exponential Growth: The Power of Compounding

Many of us recall our first job rather fondly – primarily because of the power that the sense of financial independence gave us. We may have done different things with the first salary – maybe blown it all off celebrating. Or for those with a practical bent and the need for sustenance, we may have done the appropriate acts towards picking up a rental home or buying much needed clothes etc.

The rare few (and potentially those that are guided by a mentor in some form) set apart some amount from the first salary towards investment for the future.

While it is not essential that we focus on investment right from the first salary, the earlier in our working life that we plan for and begin executing a strategy towards investments, the more secure our financial future would be.

After quoting one of the most famous scientists of all time, I now briefly digress into high school mathematics. For those who are not mathematically inclined, please skip this sub-section with the understanding that compound interest provides better returns than simple interest via the premise of staying invested (ie) we do not take out the interest amount at the end of each period.

Firstly, the principle of simple interest. Considering a fixed principal amount (P), a fixed percentage of interest (R) and a fixed number of years (N), the interest that we gain on the principal is defined by the formula

I = PNR/100

As an example, with a principal of 1000, rate of interest 5%, over a period of 2 years the interest gained would be

I = 1000*5*2/100 = 100.

So at the end of two years our investment return would be 1100 (summing up the principal and interest).

Compound interest changes the above calculations by using the fact that at the end of year one, our principal can be increased to include the interest – this assumes that we are remaining fully invested. So if we calculate against the same example above, at the end of year 1 we have an interest value of

I1 = 1000*5*1/100 = 50

For the second year, we update the principal to include the interest so we are now operating off a base of 1000+50 and the next year’s interest can now been calculated

I2 = 1050*5*1/100 = 52.5

At the end of two years our investment return is now 1102.50

With very small amounts and periods we already see a benefit of 2.50 between simple and compound interest. As the number of years go up the difference in the benefit begins to change drastically.

To those who would like to recall the direct formula for compound interest it is

A = P(1+R/100)^N where Ais the amount of return (principal + interest)

The exponential N is what brings in the compounded return with far reaching benefits. The best illustration of compounding returns comes from the fable of the rice and chess board (alternately wheat and chess board)

In ancient India, the game of chess was invented by Sessa and after having played many a mesmerizing game, his king was extremely pleased with the invention. The king asked Sessa to name any reward that he would like for this amazing invention. Sessa’s request was quite simple. He looked to be rewarded for each square on the chessboard:

• 1 grain of rice for the first square
• 2 grains of rice for the second square
• 4 grains of rice for the third square

and so forth until all 64 squares were paid for. Primarily the amount doubled for each square. There are versions which state that it was grains of wheat, but that is immaterial to the outcome.

Legend has it that the king was rather disappointed with this request and ordered his officers to immediately comply. When the royal treasury started computing the total number of grains required, it became evident that the humongous number could not be met with the assets of the kingdom. The total number of grains required is

18,446,744,073,709,551,615

which is well over a thousand times more than the global production of rice last year

There have been various studies into what would be the total volume of said number of grains, what would be the total weight etc. However, it is the principle that we should appreciate here. One way of applying this principle to our investments is that we assume our investment potential increases over time as our earnings increase, so we should double our investment amounts at fixed intervals.

If you are feeling all gung-ho about becoming a multi-millionaire and profess to double your investment amount every year, you may want to rein in because you may be setting yourself up for an insurmountable task, especially when you hit the second half of the chess board.

Ray Kurzweil, American scientist and author is credited with coining the phrase “the second half of the chess board” in his 1999 book “The Age of Spiritual Machines: When Computers Exceed Human Intelligence” ISBN 0-670-88217-8.

When we analyze the doubling numbers, we find that so long as we are in the first half of the chessboard (until square 32) we are dealing with numbers that can be considered manageable. Square 33 in itself computes to a number that is larger than the total of the first half.

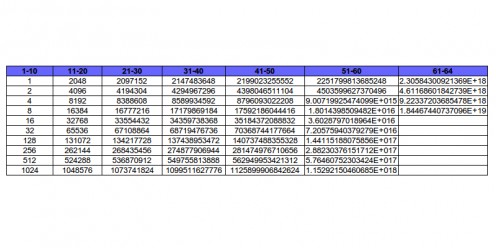
I have here an illustrated computation of the numbers computed on an excel spreadsheet (excel only gives exponentials for the last 12 due to the size of the numbers). It is clear that that the numbers in the second half are mind-boggling. Kurzweil’s use of this term was to relate to the point where an exponentially growing factor begins to have a significant economic impact on an organization's overall business strategy.

Coming back to the topic of doubling investment additions every year, obviously, looking at the numbers above, it will be infeasible after a certain point in time. However, if you succeed in doubling your investment additions even for a period of fifteen to twenty years, you are clearly on the path to become an immensely wealthy person over a period of time.

We already discussed setting aside an investment amount from each salary – the first step is to do this, and to do this consistently over the majority of your salary earning period. There is no requirement to double this amount every year, you simply increase it appropriately, as your income increases. Who decides what is appropriate? It has to be you – if you feel rich enough you can hire a financial investor to help you with the analysis.

Is that all?

Obviously, the answer is NO.

Every individual has to pick up some financial know-how – you have to understand what asset classes are available, what is the growth potential in each asset class and the associated risks. Equity and debt are two classic asset classes, there are others like property, art, precious metals. The general rule of thumb advised is to focus on equity and debt for regular investment; plan the other esoteric investments at specific points in your life. The other generic advice is to have higher equity exposure earlier in your investment career and switching over to a higher debt profile later – primarily from a risk exposure perspective.

None of these are mandatory – each person picks up their investment philosophy over time. It is also fine that you build your investment philosophy over a period of time, just keep up the act of regular investment from early on and subsequently crystallize your philosophy.

One way to use the doubling technique in your investment is to figure out the number of years it takes for your investments to double – this number would vary as per the asset class. With this number, you can build a view of how many such doubling cycles are possible within your investing lifetime and correspondingly you may wish to alter the amount invested in that asset class.

The classic error in judgment that people tend to make is to dismiss all of the topics around investment as too complex and postpone it indefinitely. Our current consumption culture also supports this – the universe of things that we can spend on during our earning days is constantly expanding and inviting. That coupled with the peer-pressure of keeping up with the Joneses tends to kick any thought of a monthly set-aside for investment right out of the window.

There are those who seek to have a fruitful employment followed by a period of retirement focused on interests and hobbies – maybe even a second career, if feasible. If you live in a country where social security is significantly mature and the national government can be counted upon to provide for your retirement, you have the best scenario possible. There may still be some tweaks that you can do to improve your social security payments, you can figure out how to address these.

For the vast majority, personal investment is a mandatory supplement to social security and there is a requirement to build up an investment corpus through the employment period. True utopia would be having an investment corpus at retirement against which you can plan your withdrawals and determine that it is adequate for the rest of your lifetime.