Angles of the Rising Sun
Sunrise
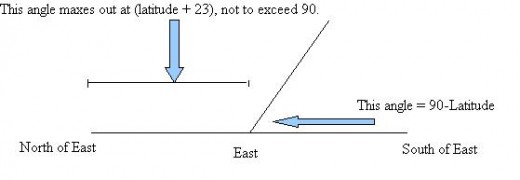
Many of you already know that the angle of the rising sun relative to the horizon is 90 degrees minus the latitude that you're observing from. If you're at the equator the sun rises perfectly vertical. If you're at 30 degrees north, it rises at a 60 degree angle. See the picture below with the arrow pointing to the angle I'm talking about.
This angle of sunrise does not depend on the season. No matter where you are at that latitude, you'll always know what angle to set your telescope at.
Now here's the tricky part to understand... How far north or south of east does it rise? On the equinoxes the sun rises perfectly east all up and down the globe. But what about during the winters and summers? If you live close to the equator you might not even notice the difference and think it always rises perfectly east. But closer to the poles you start realizing that it will rise in the north in the summer and south in the winter and the farther north you go the more pronounced the difference.
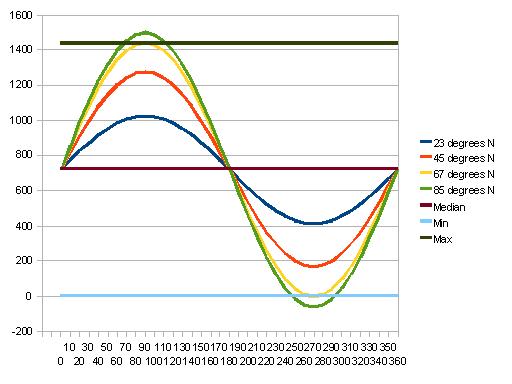
Whew! The angles aren't so obvious now, are they? Let's start with what we know: The earth's surface is curved and a logical style of math to work with would be trigonometry. The sun rises directly east on the equinoxes and that the sun is up for exactly twelve hours. If we imagine like we're at 67 degrees north we can start working with the extremes. On june 21st at 67 degrees north the sun doesn't set for a night and when the next night comes it sets and rises in the north. One thing we can derive from this isn't so obvious: the length of day approaches this extreme more slowly the closer it gets to June 21st. The days will get longer by five minutes per day in march but only thirty seconds longer per day in June.
Sunrise Angle Dependent on Latitude
Predict How Long the Sun Would Be Up
Where I'm going with this is a bit of a long shot and I'm presenting it as a question still needing confirmation.
I need to tailor an equation to predict how long the sun is up every day.
The need for this stemmed for discovering a misconception in my understanding of the sky. For a while I believed you could not see a full moon and the sun at the same time because they're on opposite sides of the earth. Some of you know from just staring at the sky that sometimes you can see both just fine. How is that possible? Well, think of angles in terms of minutes. Where the earth rotates one degree every four minutes that's 720 minutes for 180 degrees. If it's a full moon and the sun is up for more than 720 minutes then you're looking at more than 180 degrees worth of the solar plane. If you're looking at more than 180 degrees it's very possible to fit both the sun and the moon in the sky at the same time while they're 180 degrees apart from each other.
Suddenly I wanted to predict how long the sun would be up and can convert the time to angles from there. I can just read the weather report to know the time of sunrise and sunset, but I wanted to predict it myself. I needed to solve for the mathematical equation where I know the variables without reading them.
Step one: On the equinoxes the day is exactly 720 minutes long. No matter how long or short the day is at other times of year, 720 will always be in the middle between the two extremes. It's a constant to add and subtract from. And the length of day does add and subtract depending on the season. So I know I have a sine function in the equation with 720 constant
Length = 720 + Sin(X) ..... where X is the number of days to/since March 21
Note: X is an approximation. There are 360 degrees in a complete sine function and 365 days in a year. Approximating one degree a day is close enough for me.
Step two: Like I said earlier, the seasons become more pronounced when you get closer to the poles. This equation above takes into consideration the season, but not latitude. I also mentioned the days get longer faster in march than they do in June, implying another sine function in the equation.
Length = 720 + Sin(X)Sin(Y)..... Where Y is latitude.
Equation is still not complete at this stage. Those of you familiar with trigonometry know that sine functions max out at 1 and min at -1. They have to be multiplied by a constant Z to make them more extreme. I also left Y loosely defined above. We know at 67 degrees north on June 21st the sun rises directly north, and it will never rise on the west side of north. We know the length of the day on June 21st is a full 24 hours so we can write the equation like so:
1440 minutes = 720 + Z*Sin(90 days since march 21)*Sin(67 N)
Doing the math we can isolate Z and define it as 785. So the final equation that I'm postulating and awaiting feedback on is as such:
Length = 720 + 785*Sin(# days since march 21)*Sin(Lat)
Now you can substitute cosine in for sine if you use a different start date than march 21. Also you can take the length of the day in minutes and divide by 4 to get how much of the solar plane you can see at any given time. Something to also keep in mind is that when you're farther north than 67 degrees North the equation spits out a length of day greater than 1440, which is impossible. If you were to draw the function on a line, it would look like a sine function that got cut off at 1440 and 0. The image below shows this. When it's between 0 and 1440, the lines obey the hypothetical trigonometry in terms of day length and derivatives (change in length of day per day). Outside that range is either constant day or constant night. I also did not include the poles as they just have too complicated a trigonometry to handle. By the math I've described the sun actually rises and sets at an angle of zero at the poles, which throws all the math to hell.
Length of Day vs. Season Chart