- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming
Algorithms in Programming
Introduction
Welcome, In this hub I will discuss about good algorithms design and software Development. Not only good programming can make good software, the choice of the algorithm is an important aspect of good software design.
To analyze an Algorithm we take two factors into consideration, they are the Time and Space, they are measured in respect to size of the input into the algorithm. Computers are supposed to solve complex problems with relatively large inputs.
I will discuss the importance of Algorithm Design for a computer program.
Computer Algorithm
An algorithm is a description of a sequence of activities that constitute a process of getting the desired outputs from the given inputs. An algorithm when expressed in a language understood by a computer is a computer program.
An algorithm should have the following characteristics:
1. Finiteness : it should have terminate in a finite number of steps
2. Definite: Each step should be precisely defined.
3. Effective: Each step should be sufficiently basic to understand.
4 Input and 5. Output: for a given input the algorithm produces a precise output.
Why study Algorithm
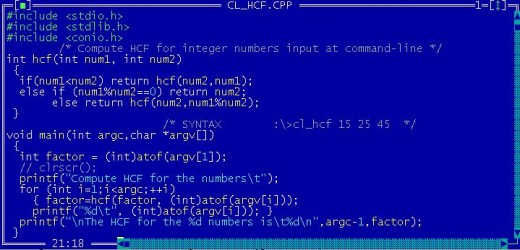
Let us consider an algorithm to compute the GCD / HCF of two numbers.
Algo1. using the basic definition
Input n1,n2; Min=iif(n1<n2,n1,n2) for i=Min to 1 step -1 if n1 mod i ==0 and n2 mod i ==0 then return i; break else continue
Algo2: the Euclid algorithm, the intelligent method.
Algo3: factorizing and grouping we studied at school.
There are many more algorithms iterative and recursive, we can code to make the work done. We know a few Sorting algorithms; Now, the question arises Which algorithm will be better than the other, this comes to the study on Analysis of Algorithms.
The algorithm which produces its output in less time for all expected inputs on a standard computer is obviously better. But, how shall me measure it?
Generally, the resources that are taken into consideration for analyzing algorithm include:
1. Time expected to be taken in executing the instances of the problem generally as a function of size of the instance. we say the Time Complexity of the algorithm.
2. Memory space expected to be required by the computer system in executing the instances of the problem generally as a function of the size of the instances. we say the Space Complexity of the algorithm.
We can write algorithms for our problems in recursive manner or using the iterative approach. There are many well known techniques for designing an algorithm say 1. Divide & Conquer, 2. Dynamic Programming, 3. Greedy approach, 4. Search and traversals, 5. Back Tracking, 6. Branch and Bound.
After the study of an algorithm, good Data Structure choices makes the efficient computer program.
Asympototic Bounds
These are the mathematical functions and notations for the Analysis. I will not be discussing the Asymptotic Analysis nor defining them in this blog, but I shall be using the Asymptotic analysis to analyze the algorithms discussed later. Please check the web for well known asymptotic functions and notations.
The approaches for determining the complexity for executing an algorithm can be empirical or theoretical. In the view of the advantages of the theoretical approach we shall use it as the only approach for computing complexities of algorithms.
Analysis of Algorithms
As, I do not want to be much theoretical, I shall not write the complete algorithms to explain the concepts discussed, and I did not earlier either; but I will discuss the main concept behind the actual algorithm. I would therefore expect everyone reading this blog having some programming experience with the knowledge of computing.
Problem1. Consider a program to find, if the given input number n is a Prime number.
to solve the problem we normally use a loop starting from 2 to the number n-1, computing the mod at each iteration and break the loop if n is found to be a composite number. Clearly, the for-loop executes at-most n times which is obvious in the worst case.
Do we need at-most n iterations in average case? We can first check if the number is even, and increment the loop step by 2 instead of 1 step, thus checking for divisibility by 4,6,8,10...even numbers would not be necessary. Now, making this slight modification to our algorithm would execute in n/2 +1 steps even in worst case which is better.
This can be improved further? We know that if a number n is divisible by a (integer of course) then there also exists another integer b by which n is divisible, and the relation is given by a * b =n; if a , b are distinct then the relation between a & b is either a>b or a<b. Now, we can easily terminate the loop when the loop-counter reaches square-root-of number n. Thus our algorithm performs much better O(√n) even at worst case compared to O(n).
int number, factor;
printf("Input a number"); scanf("%d", &number);
if (number==2 || number==3)
{printf("The number is a Prime number"); getch(); exit(0);}
else
if (number%2==0)
{printf("The number is a even number"); getch(); exit(0);}
for (factor=3;;factor+=2)
{
if (number%factor==0)
{printf("The number is a composite number"); break;}
else
if (factor*factor>number)
{printf("The number is Prime"); break;}
}
more examples on algorithm Analysis
In the next example, I will discuss the problem of computing prefix average.
The input is a single dimension array A of n elements, the output is the array B where for every element i in B is the average of the elements 1 to i of array A.
this is : B[i]=(1/i)∑A[k] for k=1 to i.
We can compute B[i] for every i, that is at every step of i the array A from index 1 to i is computed, and assigned to B[i]. here we will need two nested loops which results the total operations is a quadratic function of input size n. We can modify the algorithm to a linear algorithm by simply avoiding to compute the partial sums repeatedly.
for i=1 to n sum=sum+A[i] B[i]=Sum/i end for
Problem 3. Computation of the Exponent of a number
lastly explaining this problem using an example rather than theoretically defining it.
Suppose I want to compute 5 to the power 15, So instead of computing 5*5*5*5*5*5*5*5*5*5*5*5*5*5*5 14 multiplication steps, ((((5^2)^2)^2)^2)/5 we need only 5 multiplication steps, squaring at each iteration.
In the next problem on Integer multiplication the Karatsuba algorithm is faster than the known methods.
Algorithm Design
There are many more topics of interest in designing efficient algorithms, of which the following topics of interest shall be discussed later on this blog.
The topis of Interest I would like to discuss are, Please check the web for further information.
1. Divide and Conquer
2. Randomization
3. Greedy Technique
4. Dynamic Programming
5. Graph Algorithms
and finally 6. Algorithmically Unsolvable problems.
I hope I was able to give an introduction regarding the importance of algorithm analysis and design of good computer programs. Hope you enjoyed the reading.
© 2012 Dipankar Basu