- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming
C++ Program to Find If a Number Is Prime or Not
Below is a simple C++ code for the program to check if a given number is prime or not.
for ( int A = 2 ; A <= ( Number/2 ) ; A++ )
{
if ( Number % A == 0 )
{
cout<<"Not Prime"<<endl;
break;
}
}
cout<<"Prime"<<endl;Logic Used in Code to Find Prime Numbers
If the modulus of a number equals zero when it is divided by all the numbers between 2 and itself, at any point, then the number is Not Prime because it was found divisible.
Similarly, if the modulus does not equals zero when number is divided by all numbers between 2 and itself it means it is not divisible in the range and hence Prime.
Code Explanation:
Line 1: Initiates a for loop to divide the number with all numbers between 2 and the number itself.
Notice that the loop condition is ( number / 2 ) this is because the lower half of the values returned will be similar to the upper half of the values returned if the condition was simply set to (number). Try it if you want to confirm it.
Line 3 - 7: If at some point modulus equals zero, "The Number is Not Prime" is printed and the loop breaks.
Line 9: If modulus is not found to be zero, "Prime" is printed.
The above code can be incorporated into a function which we can call 'Prime Checker'.
Function to Check if a Number is Prime or Not.
#include <iostream>
#include <cmath>
using namespace std;
int Primechecker ( int Number )
{
if ( Number < 1000 )
{
for ( int A = 2 ; A <= ( Number/2 ) ; A++ )
{
if ( Number % A == 0 )
return (0);
}
return (1);
}
else
cout<<"invalid Nos"<<endl;
}Line 1 - 4: Formalities for starting a code, I guess you already know why they are included.
Line 6: Declares a function called 'Primechecker' with integer 'number' as its parameter which means that this function will use the value assigned to integer 'number' ( value can be assigned in the main body). Return type of this function is also integer which specifies that a function will return an integer after completing its task.
Line 8: Sets a condition that the number entered must be less then 1000 (not a necessary step).
Line 12 - 13: If at some point, modulus equals zero, a zero is returned ie. A false is returned and loop terminates, functions exits.
Line 15: If modulus is not found to be zero at any point loop continues to execute and when its execution is completed one is returned ie. True.
Now, let's look at the main body of the program where we will be calling our function and put it to some use.
int main ()
{
int Number;
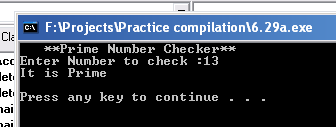
cout<<" **Prime Number Checker**\n";
cout<<"Enter Number to check :";
cin>>Number;
if ( Primechecker ( Number ) )
cout<<"It is Prime"<<endl;
else
cout<<"Not Prime"<<endl;
cout<<endl;
system ("pause");
}
Line 9: If the function is found to be true the number is Prime.
Line 11: Else it is Not Prime.
C++ Program to Find and Print Prime Numbers from 0 to 10,000
We can slightly modify the same code to print all the prime numbers that are present within a specified range of 0 - 10,000. We will use the same function described above in the main body.
Logic Used in Code:
Call the function inside a for loop and increment it up till your desired range. The program will check each number within that range and if it is Prime it will be printed else the loop will continue.
int main ()
{
int Number = 2;
cout<<" **Prime Number Checker**\n";
cout<<"Numbers found Prime are :"<<endl;
for ( Number = 2 ; Number < 10000 ; Number++ )
{
if ( Primechecker ( Number ) )
cout<<Number<<endl;
else
continue;
}
cout<<endl;
system ("pause");
}Line 8 - 9: Initiates a for loop. The condition in the for loop is the number up to which you want prime numbers to be printed.
Line 13: The continue statement instructs the loop to continue incrementing when the condition in if statement is not found to be true i.e when a number is not found to be prime.
This article is accurate and true to the best of the author’s knowledge. Content is for informational or entertainment purposes only and does not substitute for personal counsel or professional advice in business, financial, legal, or technical matters.
© 2014 StormsHalted