Computer Graphics - Transformations, Clipping and Rasterization
What is a Transformation?
A transformation is the process of mapping points to other locations. Common transformations are Translation, Scaling and Rotation.
3D Rotations
3D rotation sequence:
- Translate the object so that the rotation axis passes through the coordinate origin
- Rotate the object so that the axis of rotation coincides with one of the coordinate axes
- Perform the specified rotation about the selected axis
- Apply inverse rotations to bring the rotation axis back to its original orientation
- Apply the inverse translation to bring the rotation axis back to its original spatial position
What is Clipping?
Clipping is the process of determining the portions of a primitive lying within a region called
the ‘clipping region’. Types of clipping are Point clipping, Line clipping, Polygon clipping.
What is the purpose of Clipping?
It is for preventing:
• Activity in one window from affecting pixels in other windows
• Mathematical overflow and underflow from primitives passing behind the eye point or at great distances (in 3D)
Area Clipping
• Clipping a line segment yields at most one line segment
• Clipping a polygon can yield multiple polygons (However, clipping a convex polygon can yield at most one other polygon)
Rasterization
Rasterization (scan conversion) is to determine which pixels that are inside a primitive specified by a set of vertices.
• To convert continuous geometry, inside viewing region, into discrete pixels
• Fragments have a location (pixel location) and other attributes such color and texture coordinates that are determined by interpolating values at vertices
• Pixel colors determined later using color, texture, and other vertex properties
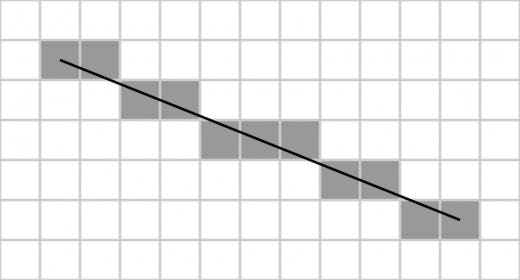
Line-Drawing Algorithms
Bresenham’s line algorithm properties:
- Only uses incremental integer calculations
- Can be adapted to display circles and other curves
- Basic idea find next pixel from current one
Area Fill
Boundary fill
Start at an inside position and ‘paint’ the interior, pixel by pixel, with the desired colour until the boundary colour is encountered
Flood fill
• Start at an inside position and ‘repaint’ all pixels that are currently set to a certain colour with the desired colour