Computer Models: An Abstraction of Realty
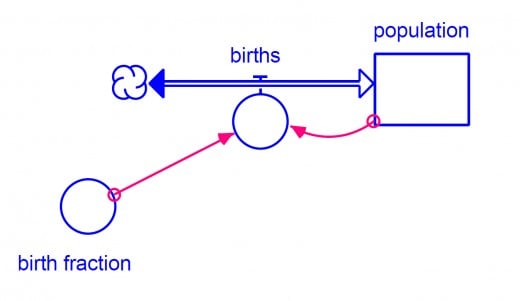
Every computer model is an abstraction of realty. This is by definition. Models are created by taking pieces of reality and putting them together in a form that can make some sort of prediction or assessment about something. Models are usually designed to represent reality but it is not reality itself.
To use an example we can look that the population dynamics of a town. In its most simplest a basic form, the town's population can be represented by the difference between the birth rate and death rate. This is an abstraction of realty because we know that there are many more factors that influence population levels than just the birth rate and death rate. What's important to note here is that even when you add more parameters to a model to increase its accuracy and realism (such as the rate of people moving into and out of town), it's still just an abstraction on realty. Think of it this way, a model may approach reality as the accuracy and number of variables increases but it will never become reality.
Another example could be a hydraulic model of complex drainage system. There are a multitude of modeling programs that can be used to create a simulation of the drainage system. The hydraulic engineer can choose the modeling approach, define parameters to describe the system (such as channel dimensions, rainfall depth and intensity, ground cover, etc) and then let the computer crunch the numbers. The results that may be produced could include such things as the depth of flooding, flood velocities, inundation limits, etc. However, no matter how complex or how many finite elements are used to define the model's features, it is still only an abstraction of reality.
Because every model is an abstraction of reality, every model has a boundary as well. A model's boundary is essentially its limit. That is to say that a boundary can be starting point in a model, an ending point, or simply the interface between something being modeling and something on the "outside." In addition to this, every model must have a boundary - you can't have a model without one. Even the most sophisticated computer models have a boundary and require an initial conditions to set the simulation in motion. All models have a starting point and require some kind of seed to set the simulation in motion.
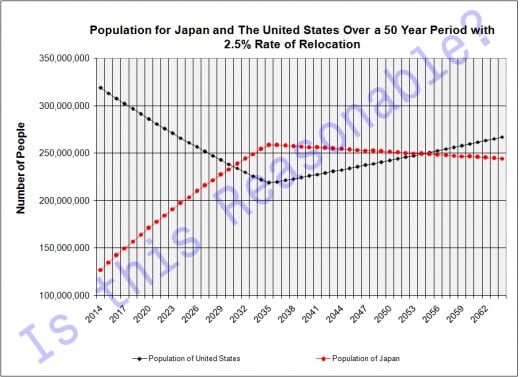
Can Any Model Be Useful Then?
Even though models are abstractions, they can still be quite useful. In fact, even simple models can be useful in such applications as business, engineering, healthcare, etc. However, the usefulness of model and its results are depended on a number of factors. First, you have to consider what your inputs to the model are. If you use garbage data to start the model, then it most certainly will give garbage results (the famous GIGO acronym - Garbage In Garbage Out). So then therefore it becomes very important to ensure that your model inputs are accurate an representation of the situation you are trying to model.
Once your model has produced results you should diligently review to check for reasonableness. This initial test of reasonableness is often called the "smell test." The "smell test" is a common sense way of evaluating the results of a model. Essentially, if the model produces impossible values (such as a town's population exceeding the world's population) or negative values for parameters that should never go below zero, then the model doesn't pass the "smell test."
If something doesn't pass the "smell test" (and you are certain that your inputs are good) then it usually means that there is an error in the model or that something important is missing. The error could be anything from a simple mathematical error to the failure to include a parameter in the model that would have an impact on the results. In essence, the "smell test" is a way of assessing the adequacy of a model without actually doing an validation or calibration.
Model Confidence
Confidence in a model is fairly subjective and differs from one model to another depending on a variety of factors. Obviously, confidence is tied to the perceived accuracy of the model that is being run. If a model has been validated using real life data then we would be expected to have a good degree of confidence in that model. Furthermore, if a model has been tested to accurately predict a variety of real life situations, then we would be expected to have a high degree of confidence in the model as well
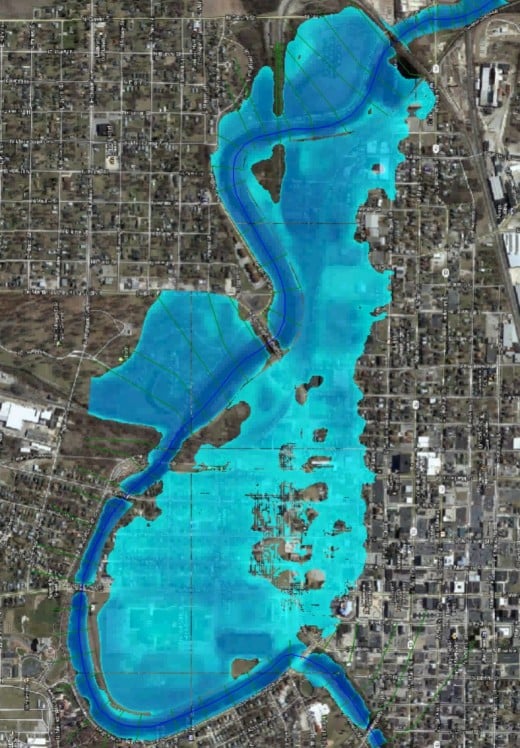
Validating models is an important step to help ensure that the results can be trusted and that they would be useful. Validation takes many forms but typically includes comparing results of the model to real life measured values. For example, a flood inundation model's predicted depths can be compared to water marks from an actual flood. If the computed flood depths match the measured flood depths (and the parameters to describe the drainage system are accurate) then the model can be assumed to produce accurate results. Going back to the example of a model describing the population dynamics of a town, the predicted population at any given moment in time can be compared to a census to validate (or invalidate) the model.
In addition to having model validation, a key to confidence in modeling lies in the documentation. If any model is to be used to properly, the user should consult the documentation of that model first. It's import to do this so that you are aware of a model's assumptions and limitations. Additionally, it's important to review the equations that the define the relationships of variables within the model as well as this may influence the types of outcomes that it produces.








