- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming
Graph Traversals
Graph Traversal
Generally, traversing a graph means visiting all the vertices of the graph exactly once, which can start at any vertex. Several graph traversing algorithms have been developed; I shall discuss two graph traversal algorithms here. The DFS and the BFS.

Depth First Search
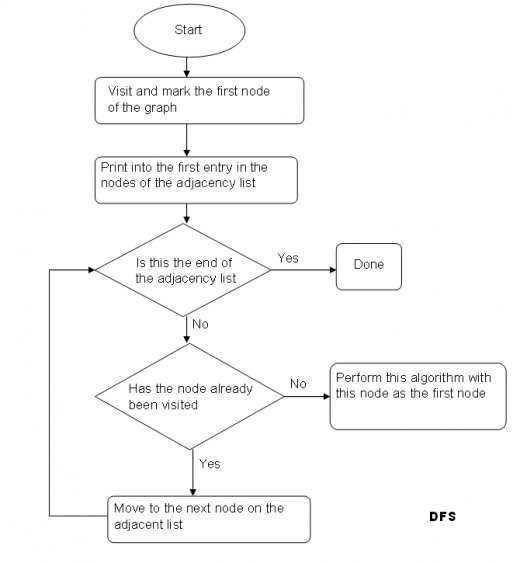
In DFS we visit the starting vertex V first, then visit all the vertices that lie along a path which begins at V, i.e. the vertex immediate adjacent to V (say Vx), Next, if Vx has any adjacent vertex (say Vy), then visit it and continue till there is a dead end. When a vertex is explored down to leaf, we backtrack to explore the remaining adjacent vertices and this continues until all vertices are discovered. We use the data structure STACK to traverse in DFS. The idea of this algorithm is to make a path as long as possible, and then backtrack to add branches also as long as possible.
We can also use the DFS traversal for topological sorting of a directed acyclic graph.
Flowchart

Breadth First Search
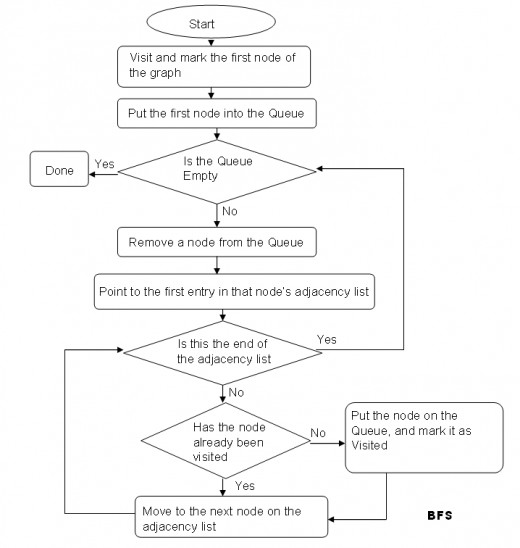
In BFS we start with the starting node A, then we examine all the neighbors of A, then we have to examine all the neighbors of the neighbors of A, and so on. We need to keep track of the neighbors of a node, and this can be done using the data structure QUEUE. First it discovers every vertex adjacent to V, and then systematically for each of those vertices it finds all the vertices adjacent to them.
Informally, we explore all connected vertices and add the visited vertices into queue; next, we remove item from the queue and repeat on the popped item. This is iterated until the queue is empty which makes the traversal complete.
Flowchart
Example
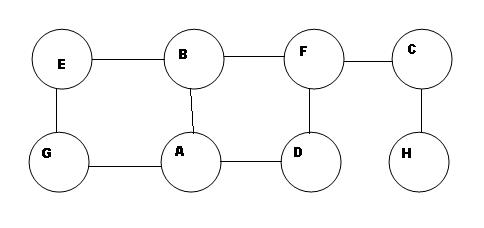
BFS
VISIT starting vertex A
adjacent to A unvisited vertices are B, D, G
VISIT B and ENQUEUE B
VISIT D and ENQUEUE D
VISIT G and ENQUEUE G
DEQUEUE B
adjacent unvisited vertices of B are E, F
VISIT E ad ENQUEUE E
VISIT F and ENQUEUE F
DEQUEUE D
no unvisited adjacent vertices of D remains so DEQUEUE G
no unvisited adjacent vertices of G remains so DEQUEUE E
no unvisited adjacent vertices of E remains so DEQUEUE F
adjacent unvisited vertices of F is C
VISIT C and ENQUEUE C
DEQUEUE C
adjacent unvisited vertices of C is H
VISIT H and ENQUEUE H
DEQUEUE H
there is no unvisited adjacent vertices of H and the Queue is Empty so End
The BFS is A B D G E F C H
DFS
VISIT starting vertex A and PUSH A into STACK
unvisited vertices adjacent to A is B, D, G
we VISIT B and PUSH B
unvisited vertices adjacent to B is E, F
we VISIT E and PUSH E
unvisited vertices adjacent to E is G
so VISIT G and PUSH G
no adjacent unvisited vertices of G remains so POP stack
no adjacent unvisited vertices of E remains so POP stack
unvisited vertices adjacent to B is F
VISIT F and PUSH F
unvisited adjacent to F is C, D
we VISIT C and PUSH C
next, we VISIT H and PUSH H
no adjacent unvisited vertex of H exists so POP stack
no adjacent vertices of C remains unvisited so POP stack
unvisited vertices adjacent to F is D
so, VISIT D and PUSH D into the stack
no adjacent vertices on top of stack remains unvisited so POP the stack
The DFS is A B E G F C H D
© 2012 Dipankar Basu