Mathematical Analysis Of The Behavioural Properties Of Inflatable Dams
Available Methods Of Analysis
Inflatable dams present considerable difficulties from the viewpoint of analysis, because the membrane shape under load is not initially known. However, mathematical analysis of the behavioral properties of inflatable dams, had been produced by Anwar(1), Harrison(2), Parbery(3) and others. The approaches of analysis developed by the first three above are mentioned in brief in the succeeding sections. In Chapter Three(next hub), the procedures of numerical analysis based on Harrison's and Parbery's methods are given in more details.
Anwar's Method
The analysis given by Anwar for both air inflated and water inflated dams, consider the case where upstream water level is at the crest of the dams and apply to the idealised weightless, inextensible membrane. The length of the curved perimeter and the base length are not taken into account.
Figure (3) defines the various parts of the two dimensional model for an air inflated dam.
Figure (3)
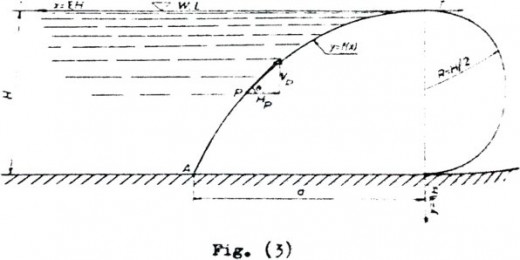
It is assumed that the inflated air pressure inside the inflatable dam is proportional to the upstream head H, that is
Pi = a.p.g.H
where Pi = internal air pressure, a = proportional factor, p = density of water and g = acceleration due to gravity.
The pressure difference on the downstream face is constant, thus the shape of the dam profile for this part is semi-circular curve of a diameter H. Considering the semi-circular downstream, the tension in it is
T = 1/2.Pi.H = 1/2.a.p.g.H2
The shape of the upstream face is calculated by considering the vertical and horizontal components of the tension at an arbitrary point P. Figure (4) shows a portion OP of the upstream face. This portion must satisfy the equilibrium condition.
Figure (4)
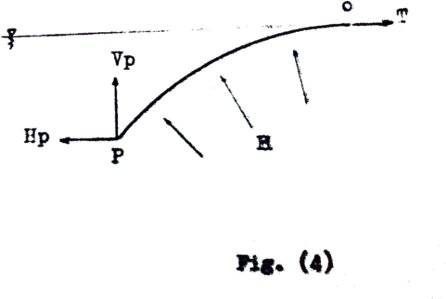
Φ αThe horizontal and vertical components of the tension acting for unit length at point P are respectively
Hp = T + (1/2).p.g.y2 - Pi.y = (1/2).a.p.g.H2 + (1/2).p.g.y2 - a.p.g.H.y
and
Vp = p.g ∫ f(x).dx - Pi.x = p.g ∫ f(x).dx - a.p.g.H.x
where f(x) is an analytical function describing the shape of the dam.
The slope at the arbitrary point P can be written as
tan θ = y' = Vp/Hp = - {(2.f(x).dx - 2.α.H.x)/(a.H2 + y2 -2.α.H.y) }
The equation above is solved in term of elliptic integrals which is expressed as follows
E = √2α { 2E(k) - F(k) -(Φ,k) + 1/2F(Φ,k)}
where k = √(α/2) , Φ = cos-1(n/α - 1) , E = x/H , and n = y/H. E and F are the elliptic integrals of the second and first kind respectively, and the circumflex denotes the integrals are complete.
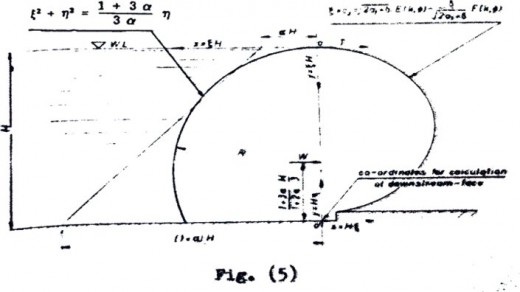
Figure (5) defines the various parts of the dimensional model for the water inflated dam. Equations for the upstream and the downstream faces are shown in the figure.
Figure (5)
Harrison's And Parbery's Methods
Harrison developed a finite element method of analysis which may be used in many practical cases. Self-weight and extensibility of the membrane material may be included in the analysis. The method can be adapted for any combination of water and air. The approach of the method is to assume that the perimeter of the dam profile is composed of a finite number of small elements of unit longitudinal length which could be treated as straight, and the load on each element as acting as concentracted loads at its extremities. The position of each element are determined by considering the equilibrium of each element and its compatibility with its neighbours in turn, beginning from the first element at the upstream fixture. This is made possible by giving the first element trial values of tension and slope. These trial values are corrected towards the true values by employing the Newton Method of iteration.
Parbery derived three differential equations which with four boundary conditions, defined the equilibrium shape of an inflatable dam. His formulation of the analysis is the equivalent in continuous form of the finite element method of Harrison. The method is also suitable for a wide range of load conditions, in which self-weight and extensibility of the membrane material may be included in the analysis. The differential equations can be integrated using a fourth order Runge-Kutta method with estimates of upstream slope and membrane tension which will then be refined also using the Newton Method of iteration.







