Converting binary and hexadecimal numbers to Decimal
Introduction
Binary numbers are bits, one's and zero's that a computer uses to represent an electronic state. Binary numbers use a base 2 value system instead of the base 10 system that is used with general arithmetic. Using a 2 base system means instead of going by powers of ten i.e. 10,100,1000 etc. the base 2 system goes 2,4,8,16, powers of 2. Binary numbers are long to write and harder to work with than the decimal number system. The number 300 in decimal is written as 100101100 so you can see this can be hard to work with. This is where the hexadecimal system comes into play. The hexadecimal system is a base 16 system, 16, 256, 4096 and so on. Because the hexadecimal system uses the base 16 system it uses about 1/4 as many digits as the binary system. The hexadecimal system uses the base numbers 0-9 and also A,B,C,D,E,F to represent 10,11,12,13,14 and 15 respectively. A chart is shown below showing the conversion values of the decimal system to the hexadecimal and binary system for numbers 0-15.
Decimal, Hexadecimal, and Binary conversion chart
Decimal
| Hexidecimal
| Binary
|
|---|---|---|
0
| 0
| 0
|
1
| 1
| 1
|
2
| 2
| 10
|
3
| 3
| 11
|
4
| 4
| 100
|
5
| 5
| 101
|
6
| 6
| 110
|
7
| 7
| 111
|
8
| 8
| 1000
|
9
| 9
| 1001
|
10
| A
| 1010
|
11
| B
| 1011
|
12
| C
| 1100
|
13
| D
| 1101
|
14
| E
| 1110
|
15
| F
| 1111
|
Converting Decimal to Binary and Binary to Decimal
There are a couple of ways to convert decimal numbers into binary numbers. There is the method of comparing descending powers of two and subtracting and there is the short division by two with remainder methods.
Binary to Decimal Descending Powers of Two and Subtraction
Using the comparing descending powers of 2 and subtraction method we will take the decimal number that you want to convert into binary and start with the highest base 2 number that will fit into it. It helps if you make a binary base 2 chart to help out.
2^0
| 2^1
| 2^2
| 2^3
| 2^4
| 2^5
| 2^6
| 2^7
| 2^8
| 2^9
|
|---|---|---|---|---|---|---|---|---|---|
1
| 2
| 4
| 8
| 16
| 32
| 64
| 128
| 256
| 512
|
Binary (base 2) Power Chart
After creating a chart for your reference then you take the decimal number you want to convert and take the biggest power of two that will fit into it and put a 1 in that spot. Since we used the number 300 earlier lets use it now.
- 29 = 512. 512 does not fit into 300 so put a 0 in that column. (left most column)
- 28 = 256. 256 fit into 300. Put a 1 in this column and subtract 300 from 256 to get 44.
- 27 = 128. 128 does not fit into 44 so put a zero into this column and continue with 44.
- 26 = 64. 64 does not fit into 44 so put a 0 into this column. Continue with 44.
- 25 = 32. 32 fits into 44. Put a 1 into this column and subtract 32 from 44 to get 12.
- 24 = 16. 16 does not fit into 12 so you guessed it. Put a zero into this column and continue with 12.
- 23 = 8 and 8 fits into 12. Put a 1 in this column and subtract 8 from 12. You are left with 4.
- 22 = 4 and 4 fits into 4. Put a one in this column and subtract 4 from 4. To get zero.
- 21 and 20 both cannot fit into zero so you can put a zero into both columns.
After all that work we should have the following 0100101100 which is 300! Good Work!
Short Division By 2 With Remainders
The short division by 2 with remainders approach is easier to utilize.
- You take the decimal number you want to convert into binary. In this case we will use 300 again and put it into and upside down division sign. )300.
- Then take 2 and use it as your divisor and put it outside of the division symbol. 2)300. Then you divide as usual and put the quotient below and the remainder to the right. Continue this process until you get 0 as a quotient
2)300r=0
2)150r=0
2)75r=1
2)37r=1
2)18r=0
2)9r=1
2)4r=0
2)2r=0
2)1r=1
0
- Go from bottom to top and write your numbers out and voila! We get the same as before! 300= 0100101100!
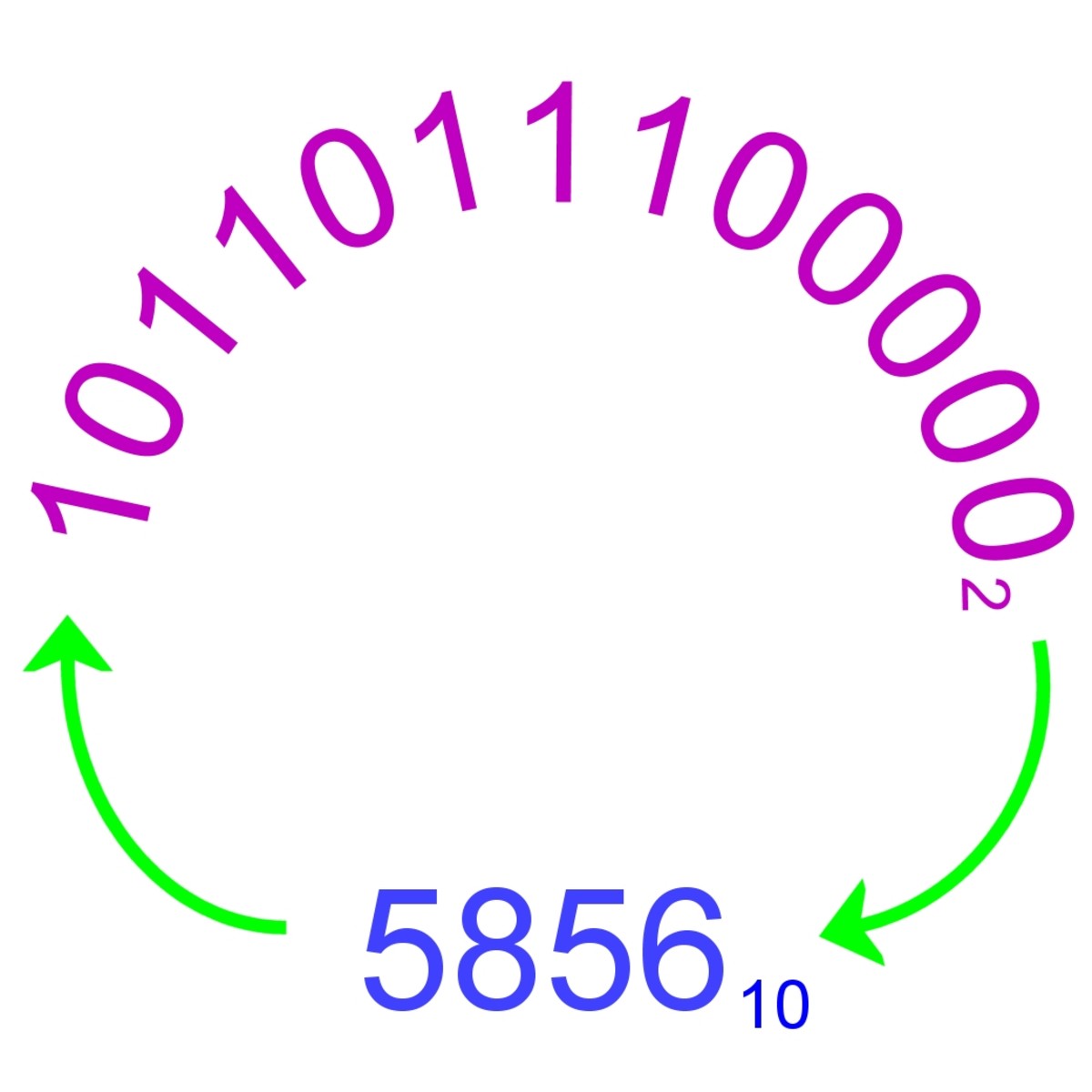
Binary to Decimal
Converting binary to decimal is fairly simple. Take you binary digits from left to right and multiply out the power of two then add them all together. We'll use 0100101100 or 300 again as we are familiar with it.
- 0*20= 0
- 0*21= 0
- 1*22= 4
- 1*23 = 8
- 0*24 = 0
- 1*25= 32
- 0*26= 0
- 0*27= 0
- 1*28= 256
- Now we add 256 +32+8+4 to get 300.
Hexadecimal to Decimal and Decimal to Hexadecimal
Hexadecimal to Decimal
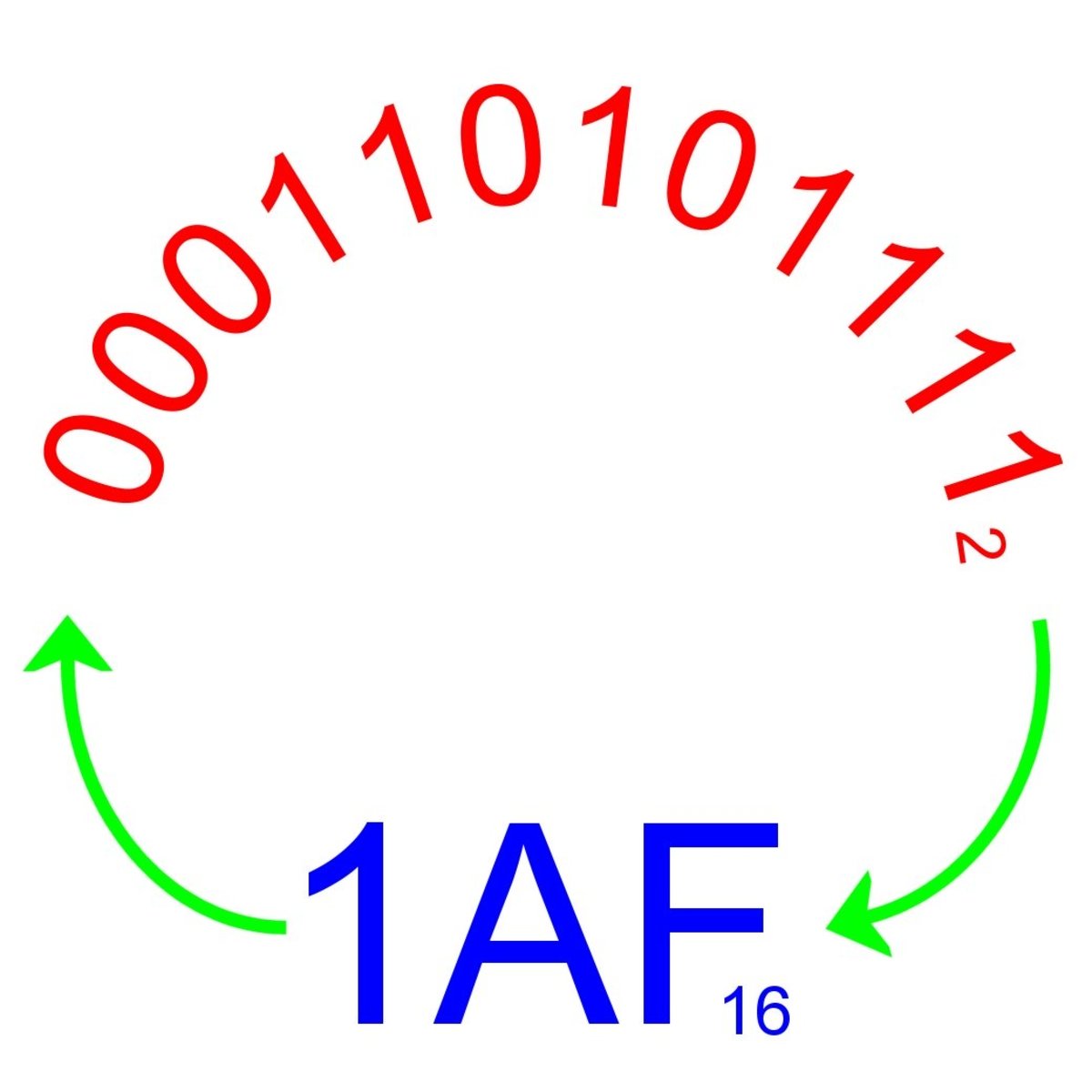
Converting hexadecimal to decimal is a simple task. Remember that hexadecimal is a 16 base system and uses the letters A,B,C,D,E,F to correspond to 10,11,12,13,14,15 respectively. We can take the hexadecimal 7F3C and convert it to decimal.
- 7 * 4096 = 28,672 ( 4096 = 163) +
- 15 * 256 = 3,840 ( F = 15, 256 = 162 ) +
- 3 * 16 = 48 ( 161 = 16) +
- 12 * 1 = 12 ( C=12, 160 = 1)
- Now we add and get 32,572. That's it we are done!
Decimal to Hexadecimal
Decimal to hexadecimal is also a lot easier than dealing with binary numbers. Here are the steps:
- Take your decimal number and divide it by 16 because hexadecimal is base 16. We can use 32,572 since we have used it before.
- 32,572/16 = 2035 with a remainder of 12 and 12 = C. C will go in the right most column.
- 2035/16 = 127 with a remainder of 3. 3 goes into the next right most column.
- 127/16 = 7 with a remainder of 15 and 15 = F. F goes into the next right most column.
- 7/16 = 0 with a remainder of 7. 7 will go into the final column since the quotient is zero we are finished.
- Our final answer is 7F3C. The same as what we started with!
Hexadecimal to Binary and Binary to Hexadecimal
Hexadecimal to Binary
Hexadecimal to binary is our next topic. Taking a hexadecimal number 4D7F to convert it to binary you simply substitute 4 bits for each hexadecimal digit.
- 4D7F in binary = 0100|1101|0111 |1111. This number is simple as you can use the chart to convert. Just remember to make sure you break each hexadecimal digit into 4 bit sections.
Binary to Hexadecimal
Binary to hexadecimal is the reverse of hexadecimal to binary. Take you binary number break it down into 4 bits each and multiply by the appropriate power of two. Lets use the example from above.
- First 4 bits = 1111 = 1*20 = 1, 1*21 = 2, 1*22 = 4, 1*23 = 8. Added together these numbers equal 15 which equals F the right most hexadecimal digit.
- Next 1110 = 1*20 = 1, 1*21 = 2, 1*22 = 4, 0*23 = 0. Added up these numbers equal 7 the next right most hexadecimal bit.
- Now we have 1011 = 1*20 = 1, 0*21 = 0, 1*22 = 4, 1*23 = 8. These numbers together give us 13 which is equivalent to D! That goes in the next right most column.
- Finally our last bit is 0010 = 0*20 = 0, 0*21 = 0, 1*22 = 4, 0*23 = 0. When added together we get 4 our final number.
Final Words
This hub page was written by me, obviously and I have done my best to keep it easy to understand. Writing informative pages for others is a benefit to me as it helps to reinforce my knowledge on topics I need to study on also. I hope that this page will be beneficial for others who would like to learn more about computer language. As I continue to learn it is my goal to publish more information to help others and help me become a better person, student and teacher. To everyone out there good luck and write well!