What's the point?
___________________
The Rope Hypothesis - An alternative to waves, particles and wave-packets
(Comments have been disabled in all my hubs. If you wish to leave a comment go to Rational Scientific Method.)
___________________
The malleable point of Mathematics is more powerful than God. We can explain anything with it. But ask the mathematician to define it and you will get to the heart of the problem. To this day they claim that the word point is 'primitive' and must remain undefined.
____________________
The chameleon of Mathematics
Is a point a dot or a location? Is it a number on a number line, an ordered pair, an event, or a singularity? Does a point have zero or two dimensions? Are there points in the real world or is this just an invention of the mathematicians? If there aren't, why do we need points to explain how Mother Nature runs her shop?
The word point is the most fundamental building block of Geometry. Mathematical physicists routinely rely on this hypothesis to explain theories such as Big Bang and annihilation. Yet the mathematicians tell you that the word point should remain undefined for else their arguments would end up being circular.
Closer inspection reveals the underlying reason the famous point remains primitive after 5000 years of history: the mathematicians cannot use the term consistently (i.e., scientifically, rationally). If they define a point as a location, they cannot use it as a brick to construct geometric figures, and if they define a point as a dynamic 'event' (Relativity), they cannot also use it as the static singularity, the alleged 'center' of a black hole. And if the point is just a number on the number line, it cannot also be an encrypted set of two numbers used to locate a point on a pair of Cartesian coordinates.
Dots are 2D objects. They OBJECTIVELY have shape and size. Locations are not objects, but rather abstract concepts. Hence, it is irrational to ascribe dimensions to a location and qualify it as 0D.
So? Is the circle of Geometry made of dots or of locations? Can we 'construct' 1D lines with either 2D dots or '0D' locations? Is it rational to say that a point is a location and then to trace a geometric figure such as a line with this concept?
Once we compel the mathematicians to stick to a definition, they find it difficult to get away with their deceptions. Their amusing conclusions are exposed for what they are: an emperor with no clothes. Is a black hole singularity an infinitesimal (> 0 size) region of infinite mass or a '0D' location with nothing in it? And how are two 'point' particles supposed to collide if they have no size or surface? How can the theorist conceive them to move in the first place if they are just locations? (Pray tell, what is a location without anything in it?) It is the versatility of the formidable word point which enables the establishment to get around the conceptual obstacles and 'explain' everything and anything.
.
What does the point have to do with Physics?
Physics deals first and foremost with objects. Philosophy deals with concepts. If the mathematical point is not a figure (i.e., a dot), it doesn't belong in Geometry to begin with. The mathematicians are in the best of cases doing Philosophy.
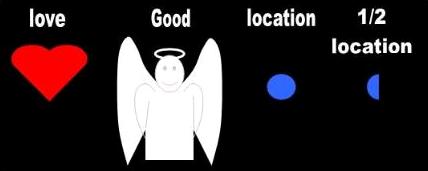
But Mathematical Physics doesn't even qualify as Philosophy. The practice of replacing a concept such as location with an object such as a dot is known as reification, a bad habit inherited from traditional religion (e.g., depicting love with a heart, Good with an angel, Evil with a snake). This places the magical chameleon of Mathematics squarely within religion. The malleable mathematical point has no place in Science because it amends itself in each sentence.
Reification
.
But the punch line is that we don't need the word point to explain any phenomenon of nature. Objectively, what we have before us is a dot. This figure is 2D: it has width and height. There are no 2D dots in nature. Nor are there such things as 0D 'point' particles. These abstract artifacts invented by the mathematicians have a strong tendency to become real when the mathematician attempts a physical interpretation of a phenomenon.
The mathematician may complain that they have no use for the genuine dot of Geometry, an insignificant blot of ink on a piece of paper, a chalk mark on the board. What good is the God of Math if we don't allow him to morph into a concept?
I'm sorry! That's OBJECTIVELY what we have before us. If the mathematicians are talking about a location, they should call it 'location' and not 'point'. The only purpose to invoke the word point is to stealthily insinuate that they are alluding to a geometric figure. The mathematical point is BOTH a physical object and an abstract concept. The mathematicians are in effect reifying the concept location when they represent 'it' with a dot. We can explain anything with such an irrational 'entity'.
_________________
.
.