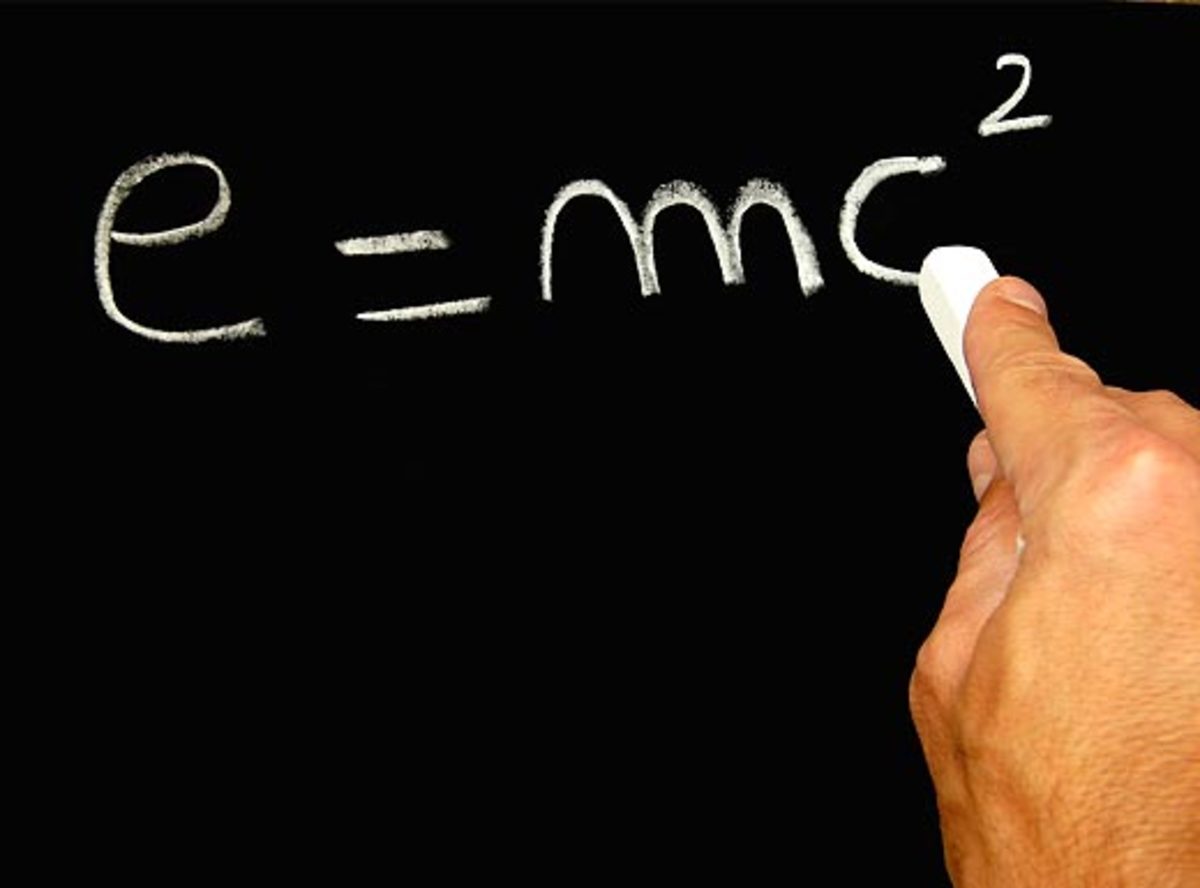A line is not the shortest distance between two points!
___________________
The Rope Hypothesis - An alternative to waves, particles and wave-packets
___________________
The line of Mathematics is one of the Seven Wonders of the Intellectual World. For unexplained reasons, the mathematicians can't define exactly what it is, but they can explain anything with it.
____________________
Will the real line please stand up?
Is a line a stick or an itinerary? Is it a geometric figure or a moving dot? Is a line a series of apples, locations, numbers? How many dimensions does a line have? Can a geometric figure only have length or be infinite? Is a line continuous? Made of discrete segments? Straight?
The mathematicians claim that they cannot define the word line because it would otherwise lead to circular arguments. They prefer to plow ahead and use the line to support their theories while insinuating that you should know what they're talking about.
Well? What ARE we talking about? What is it that we have before us?
It seems that what we have objectively on the board is a two-dimensional, elongated rectangle. Is this lackluster figure the line of Mathematics?
What we objectively have before us: a 2D elongated rectangle

The mathematicians allege that the line of Math is a wee bit more sophisticated. It has evolved considerably since the days of Euclid. The stick you are staring at is for babies. The line of Math is an exciting series of locations. It 'represents' motion. We are supposed to read into it what isn't plainly there. You are supposed to use your imagination, not your eyes.
Unfortunately for the mathematicians, Science is not in the business of deceiving audiences. A scientific dissertation has to be straight forward, without hidden meanings or unclear insinuations. Metaphor, euphemism, and figures of speech are out. Poetry is unacceptable in formal Science. The presenter points and says "line", and the audience sees a stick. What we have objectively before us is an elongated, two-dimensional rectangle. The finite geometric figure you are staring at is neither a series of location nor 'infinite' nor 1D!
The reason the mathematicians sidestep the definition of the geometric line is not a mystery. If the mathematical line alludes to an itinerary, it is not a part of Geometry, and if it consists of a series of dots, it is irrational to equate the line with numbers or with motion. Thus, the mathematicians have concocted several definitions and use them as needed to explain all of their theories, jumping back and forth, from one to another to parry the attacks of skeptics. The malleable line of Mathematics is unscientific because it cannot be used consistently. This explains why the mathematicians have never been able to define the word line precisely and prefer to tell you that it is a primitive term.

What does the line of Mathematics have to do with Physics?
The mathematicians excuse themselves saying that they cannot use the dull stick of Geometry object to sell snake oil to the masses.
The answer is that science doesn't care whether a mathematician can use the line of Geometry. This is objectively what we have before us. If the mathematicians can't use the genuine line, they should call a spade a spade! If they are referring to an itinerary they should call it an itinerary and NOT a line. If they are alluding to a series of locations they should call the aggregate motion or simply "a series of locations" and NOT a "line". By labeling a series of locations as a 'line', the mathematician intentionally misleads the juror and unjustifiably blends Mathematics with Physics. What (s)he sketches on the board are dots and what you see is a stick, but what (s)he means and insinuates is something else. You are supposed to assume that these dots represent locations. You are asked to participate in an unholy conspiracy known as reification: replacing concepts with objects. Yet (s)he continues to call 'it' a line and tells you that (s)he can scan it to make a geometric figure known as a square or that you can fit infinite dots between any two dots that make up the line!
So? Was the line used to 'construct' the square an itinerary? Was it a location, a number, or a physical dot what we were trying to fit between two 'points'?
The word line should be deleted from the dictionary of Science, among other reasons, because we don't need the word line to explain any phenomenon of nature. There are no such things as lines out there, much less if they are specified to be one-dimensional. And if the only purpose of the stick is to 'represent' an itinerary, which then is incongruously used to 'construct' a geometric figure, we can just call 'it' an itinerary. How's that for consistency?
______________
.
.