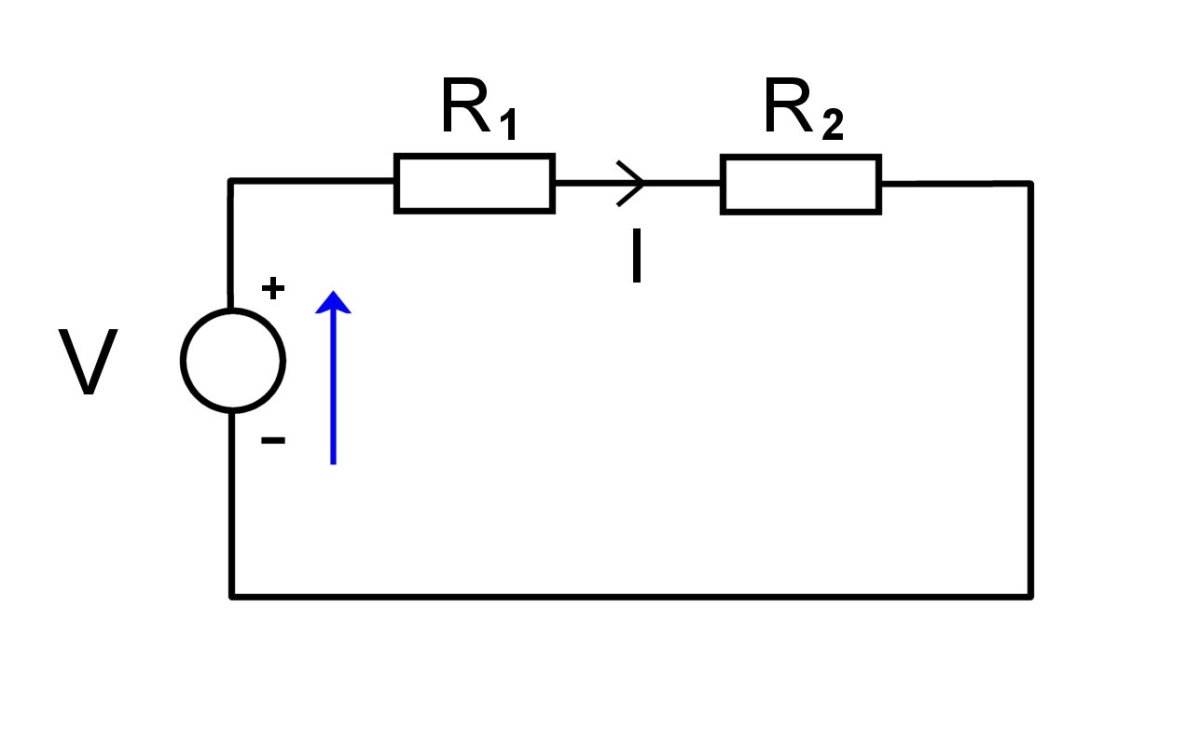
How To Analyze More Complex Series Parallel Circuits

In the last Hub, we talked about how to figure out the equivalent resistance of resistors in parallel, and in the Hub before that, we learned how to deal with resistors in series. In this Hub, we'll combine those techniques to deal with circuits that have both series and parallel combinations of resistors, whether they be series of parallel resistors, parallel combinations of series of resistors, or multiple combinations of the two. This can be done, as we'll see, through repeated application of Ohm's Law.

One method of working your way through the finding of the voltage across and current through each resistor in a complex circuit is to work your way "out" from the innermost series or parallel parts of the circuit, substituting equivalent resistances as you go, until you have simplified the circuit into a single resistor. Now using Ohm's Law, you can find the total current draw I_T of the circuit. Then, use I_T and the circuit as it looked with the equivalent resistances right before you simplified it to just a single resistor, and so on until you've worked the circuit in full. It helps to reduce the amount of recalculation you have to do by using a spreadsheet program. Having a spreadsheet is great because you can change any resistor's value and all the currents and voltages will be automatically recalculated. I'll show an example of using this technique to solve a circuit now.

Shown below is an example of a circuit with series and parallel elements. R₁ and R₂ form a series, as do R₃ and R₄. These two series are in parallel with each other, and this parallel subcircuit is in series with resistors R₅ and R₆.

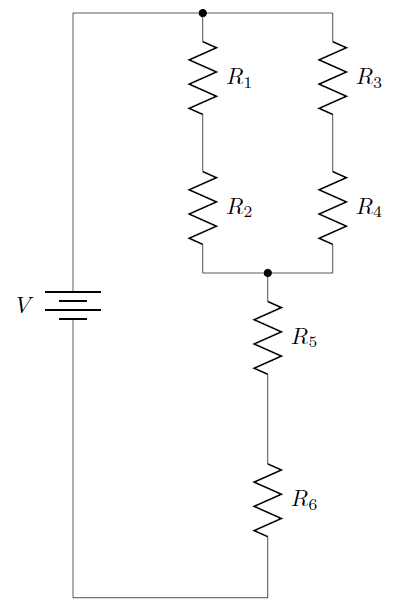
If you've got a spreadsheet program on your computer, I encourage you to follow along. Learning by doing is usually better than just passive reading!

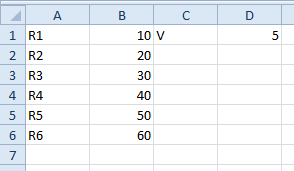
This circuit has six resistors and one voltage source. Let's put labels for the resistors R₁-R₆ in cells A1-A6 of the spreadsheet, leave cells B1-B6 for those values, put a label for the voltage source V in C1, and leave D1 for the actual voltage value. You can put in some random numbers for the resistance and voltage values (you can always change them later) so that when we set other cells for equivalent resistances and currents and voltages with formulas dependent upon these cells, we see some numbers instead of just ### or whatever your spreadsheet program shows when it can't resolve a cell's value. Shown below is my spreadsheet so far.

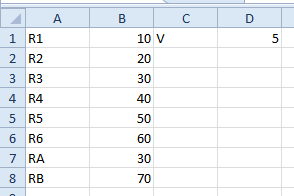
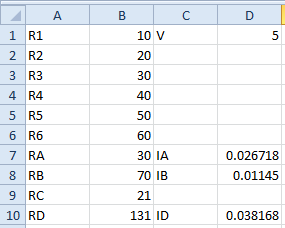
Now let's analyze the schematic. Resistors R₁ and R₂ are in series, so a single resistor called, say, R_a could be substituted where those two resistors are and it would have a resistance value equal to R₁ + R₂. So let's put at cell A7 the label RA and in cell B7 let's type in the equation '=B1+B2' (without the quotes, of course).

Similarly, looking at the schematic, we could simplify R₃ and R₄ to a single resistor called R_b with value R₃ + R₄. We put RB at cell A8 and '=B3+B4' at cell B8. Now the spreadsheet looks something like the image below.

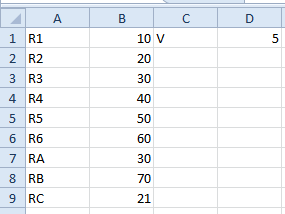
Now we can picture the two single resistors R_a and R_b in parallel with each other. What value, say we labeled it R_c, would a single resistor representing the two resistors in parallel have? If you remember from the last Hub, the formula for the equivalent resistance of two resistors in parallel is the product over the sum. So we could let cell A9 have the label RC and let cell B9 have the formula '=(B7*B8) / (B7 + B8)'. Now the spreadsheet looks like this:

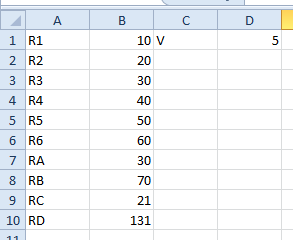
Now R_c is just in series with resistors R₅ and R₆, so we can create a cell labeled RD at A10 and its value '=B9+B5+B6' at B10, which would look like this:

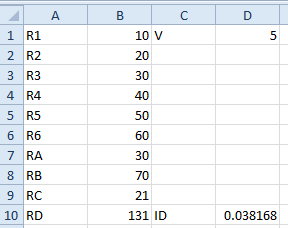
Now that we've found the total resistance of the circuit, we can work backwards to find the currents in each branch. First, let's find out the total current I_T drawn from the battery. Using Ohm's Law, we divide voltage V by resistance R_d. Since this is the current flowing through hypothetical equivalent resistor R_d, we can label the current I_d, place the label ID in cell C10, and place the value '=D1/B10' in cell D10, giving the following:

To find out how much current is flowing through the branch of R_a and how much is flowing through the branch of R_b, we can use a principle known as Kirchhoff's Current Law (KCL), discovered by German physicist Gustav Kirchhoff, which effectively states that the net current through a node is zero. In other words, what goes in must come out, and what comes out, must have come in. If X amps go out of the node through branch D, then the sum of currents coming into the node through branches A and B must be X.

How is I_d divvied up into I_a and I_b? With a two-branch setup like we have, if we want to know how much current is flowing through branch A, i.e., I_a, we divide R_b by the sum of R_a and R_b and multiply the quotient by the total current I_d. To find the current I_b flowing through branch B, we perform the same operation but with R_a in the numerator where R_b was used before.

So for IA we give the value '=(B8/(B7+B8))*D10' and for IB we give the value '=(B7/(B7+B8))*D10' as shown below:

Now that we have the branch currents for all the real branches in the circuit and the resistance of each resistor, we can use Ohm's Law in voltage solution mode (V = I * R) to find the voltage across each resistor.

R₁ is on branch a with current I_a, so V1 = R1 * IA. V2 = R1 * IA. V3 = R3 * IB. V4 = R4 * IB. R₅ and R₆ are on the branch with current I_d, so V5 = R5 * ID and V6 = R6 * ID. This is shown on the spreadsheet below:

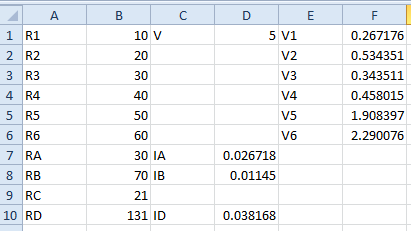
Notice that the net voltages in any closed loop through the circuit add up to zero. For instance, starting at the positive terminal of the battery with voltage V and dropping the voltages of V1 and V2 and V5 and V6, or in other words, we have V - V1 - V2 - V5 - V6 = 0. If we loop using the other branch, we get V - V2 - V3 - V5 - V6 = 0. This is known as Kirchhoff's Voltage Law. I encourage you to learn more about that! In my next Hub, we'll look at interesting circuits that can't be broken down using only series and parallel techniques. Thanks for reading!